Задача 53881 Векторная математика...
Условие
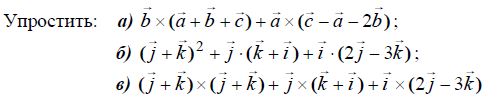
Решение
[m]\vec{b} × (\vec{a}+\vec{b} +\vec{c} )+\vec{a} × (\vec{c}-\vec{a} -2\vec{b} )=\vec{b} ×\vec{a}+\vec{b} × \vec{b}+\vec{b} ×\vec{c}+\vec{a} × \vec{c}-\vec{a} ×\vec{a}-2\vec{a} × \vec{b}=\vec{b} ×\vec{c}+\vec{a} × \vec{c}-3\vec{a} × \vec{b}[/m]
так как
[m]\vec{b} × \vec{b}=\vec{a} × \vec{a}=0[/m]
[m]\vec{a} × \vec{b}=-\vec{b} × \vec{a}[/m]
2)
[m]=(\vec{j}+\vec{k}) \cdot (\vec{j}+\vec{k})+\vec{j} × (\vec{k}+\vec{i})+\vec{i} × (2\vec{j}-3\vec{k})=\vec{j}\cdot\vec{j}+2\vec{j}\cdot \vec{k}+ \vec{k} \cdot \vec{k}+\vec{j} ×\vec{k}+ \vec{j} ×\vec{i}+2\vec{i} ×\vec{j}-3\vec{i} ×\vec{k}=[/m]
По определению скалярного произведения
[m]\vec{j}\cdot\vec{j}=|\vec{j}|\cdot|\vec{j}|\cdot cos 0^{o}=1\cdot 1\cdot 1=1[/m]
[m]\vec{j} ×\vec{i}=|\vec{j}|\cdot|\vec{i}|\cdot cos 90^{o}=0[/m]
По определению векторного произведения
[m]\vec{j} ×\vec{k}=\vec{i}[/m]
[m]\vec{j} ×\vec{i}=-\vec{k}[/m]
[m]\vec{i} ×\vec{k}=-\vec{j}[/m]
[m]=1+0+1+\vec{i}-\vec{k}+2\vec{k}-3(-\vec{j})=2+\vec{i}+\vec{k}+3\vec{j}[/m]
3)
[m]=(\vec{j}+\vec{k}) × (\vec{j}+\vec{k})+\vec{j} × (\vec{k}+\vec{i})+\vec{i} × (2\vec{j}-3\vec{k})=0+\vec{j} ×\vec{k}+ \vec{j} ×\vec{i}+2\vec{i} ×\vec{j}-3\vec{i} ×\vec{k}=[/m]
так как
[m]\vec{b} × \vec{b}=\vec{a} × \vec{a}=(\vec{j}+\vec{k}) × (\vec{j}+\vec{k})=0[/m]
тогда
[m]=\vec{i}-\vec{k}+2\vec{k}-3(-\vec{j})=\vec{i}+\vec{k}+3\vec{j}[/m]