Задача 53874 Помогите плииииизззззззз...
Условие
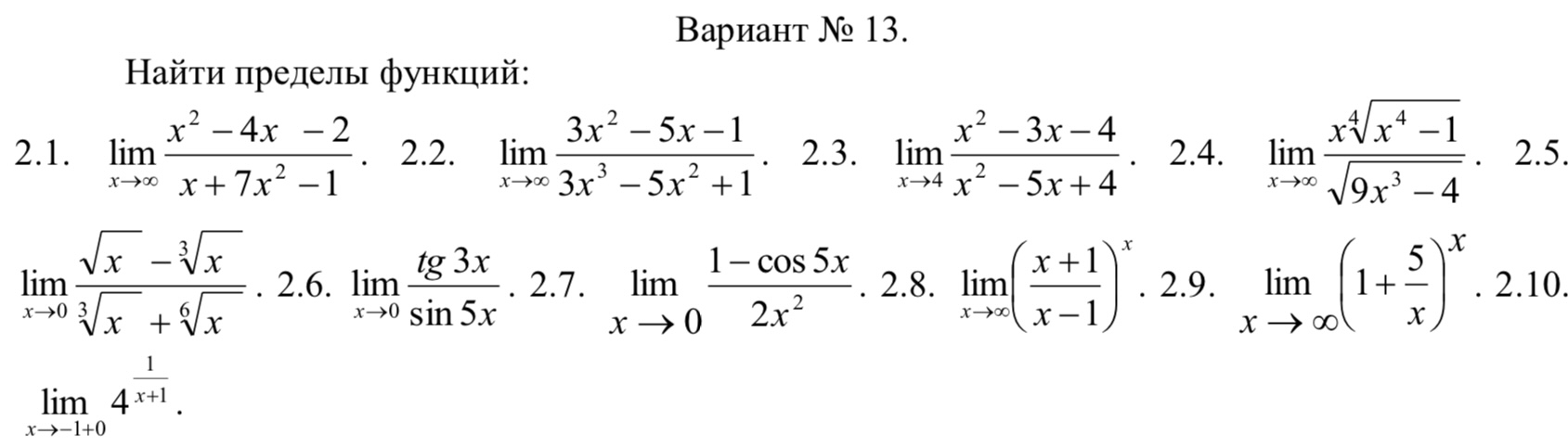
Решение
[m]=\lim_{x \to \infty }\frac{x^2-4x-2}{x+7x^2-1}=[/m]
Неопределенность ( ∞ / ∞ )
Делим числитель и знаменатель на x^2:
[m]=\lim_{ \to \infty }\frac{\frac{x^2-4x-2}{x^2}}{\frac{x+7x^2-1}{x^2}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на x^2 и
каждое слагаемое знаменателя делим на x^2:
[m]\lim_{ \to \infty }\frac{\frac{x^2}{x^2}-\frac{4x}{x^2}-\frac{2}{x^2}}{\frac{x}{x^2}+\frac{7x}{x^2}-\frac{1}{x^2}}=[/m]
[m]=\lim_{ \to \infty }\frac{1-\frac{4}{x}-\frac{2}{x^2}}{\frac{1}{x}+7-\frac{1}{x^2}}=\frac{1-0-0}{0+7-0}=\frac{1}{7}[/m]
2)
[m]=\lim_{x \to \infty }\frac{3x^2-5x-1}{3x^3-5x^2+1}=[/m]
Неопределенность ( ∞ / ∞ )
Делим числитель и знаменатель на x^3:
[m]=\lim_{ \to \infty }\frac{\frac{3x^2-5x-1}{x^3}}{\frac{3x^3-5x^2+1}{x^3}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на x^3 и
каждое слагаемое знаменателя делим на x^3:
[m]\lim_{ \to \infty }\frac{\frac{3x^2}{x^3}-\frac{5x}{x^3}-\frac{1}{x^3}}{\frac{3x^3}{x^3}-\frac{5x}{x^3}+\frac{1}{x^3}}=[/m]
[m]=\lim_{ \to \infty }\frac{1-\frac{5}{x^2}-\frac{1}{x^3}}{3-\frac{5}{x^2}+\frac{}{x^3}}=\frac{0-0-0}{3-0+0}=0[/m]
3)
[m]=\lim_{x \to 4 }\frac{x^2-3x-4}{x^2-5x+4}=\frac{4^2-3\cdot 4-4}{4^2-5*4+4}=\frac{0}{0}[/m]-Неопределенность
Раскладываем на множители и числитель и знаменатель:
[m]=\lim_{x \to 4}\frac{(x-4)(x+1)}{(x-4)(x-1)}=[/m]
сокращаем на (х-4)
[m]=\lim_{x \to 4}\frac{x+1}{x-1}=\frac{4+1}{4-1}=\frac{5}{3}[/m]
4) О т в е т. ∞
Степень числителя вторая, степень знаменателя (1,5) степень числителя больше.
Деление на х^2 ( как в примере 2) приведет к тому, что в знаменателе будет 0, в числителе число)
число/0= ∞
5)
[m]\frac{0}{0}[/m]-Неопределенность
Вынесем за скобки [m]\sqrt[6]{x}[/m]
[m]=\lim_{x \to 0 }\frac{\sqrt[6]{x}\cdot (\sqrt[3]{x}-\sqrt[6]{x})}{\sqrt[6]{x}\cdot(\sqrt[6]{x}+1)}=[/m]
сокращаем на [m]\sqrt[6]{x}[/m]
[m]=\lim_{x \to 0 }\frac{\sqrt[3]{x}-\sqrt[6]{x}}{\sqrt[6]{x}+1}=\frac{0-0}{0+1}=0[/m]
6)
[m]=\lim_{x \to 0}\frac{tg 3x}{sin 5x}=\lim_{x \to 0}\frac{tg 3x}{3x}\cdot \frac{5x}{sin5x}\cdot \frac{3}{5}=\frac{3}{5}[/m]
7)
[m]=\lim_{x \to 0}\frac{1-cos 5x}{2x^2}=\lim_{x \to 0}\frac{sin^2\frac{5x}{2}}{x^2}=\lim_{x \to 0}\frac{sin\frac{5x}{2}}{\frac{5x}{2}}\cdot\frac{sin\frac{5x}{2}}{\frac{5x}{2}}\cdot \frac{5}{2}\frac{5}{2}=\frac{25}{4} [/m]
8)
[m]=\lim_{x \to 0}(\frac{x+1}{x-1})^{x}=[/m]
Делим и числитель и знаменатель дроби [m]\frac{x+1}{x-1}[/m]на х
[m]=\lim_{x \to 0}(\frac{1+\frac{1}{x}}{1-\frac{1}{x}})^{x}=\frac{e}{e^{-1}}=e^2[/m]
9))
[m]=\lim_{x \to 0}(1+\frac{5}{x})^{x}=\lim_{x \to 0}((1+\frac{5}{x})^{\frac{x}{5}})^{\frac{5}{x}\cdot x}=e^{5}[/m]
10)
[m]=\lim_{x \to -1+0}(4)^{\frac{1}{x+1}}=(4)^{\frac{1}{-1+0+1}}=4^{+\infty}=+\infty[/m]
Не буду впредь решать такие большие задания...
Задавайте один - два примера в вопросе...