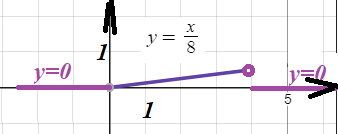Задача 53810 Непрерывная случайная величина задана...

5f729d015e684a139991de1e

2 октября 2020 г. в 08:30

Непрерывная случайная величина задана функцией распределения F(x). Найти:

1) плотность распределения и построить кривую распределения;
2) числовые характеристики случайной величины;
3) вероятность попадания случайной величины в интервал (a, b).

5f3ea7e3faf909182968ddd9

2 октября 2020 г. в 16:36

★

1.
[m]f(x)=F`(x)=\left\{\begin{matrix}0, x \leq0
\\ \frac{x}{8} , 0 < x < 4\\ 0, x \geq 4\end{matrix}\right.[/m]

2.
cм. рис.

3.
[m] M ( X)= \int ^{+\infty}_{\infty} xf(x)dx=\int ^
{0}_{-\infty}x\cdot 0 dx+ \int ^{4}_{0} x\cdot \frac{x}{8}dx+\int ^{+\infty}_{4} x\cdot 0 dx=[/m]

[m]= 0+\int ^{4}_{0} (\frac{x^2}{8})dx+0=(\frac{x^3}{24})| ^{4}_{0}=\frac{64}{24}=\frac{8}{3}[/m]


[m] M ( X^2)= \int ^{+\infty}_{\infty} xf(x)dx=\int ^
{0}_{-\infty}x\cdot 0 dx+ \int ^{4}_{0} x^2\cdot \frac{x}{8}dx+\int ^{+\infty}_{4} x\cdot 0 dx=[/m]

[m]= 0+\int ^{4}_{0} (\frac{x^3}{8})dx+0=(\frac{x^4}{32})| ^{4}_{0}=8[/m]

[m] D(X)=M(X^2)-(M(X))^2=8-(\frac{8}{3})^2=\frac{8}{9} [/m]
4.

[m]P(a \leq X \leq b)= F (b)-F(a)[/m]

[m]P(1 \leq X \leq \frac{7}{2})= F (\frac{7}{2})-F(1)=\frac {(\frac{7}{2})^2}{8}-(\frac{1^2}{8}) = [/m]считайте