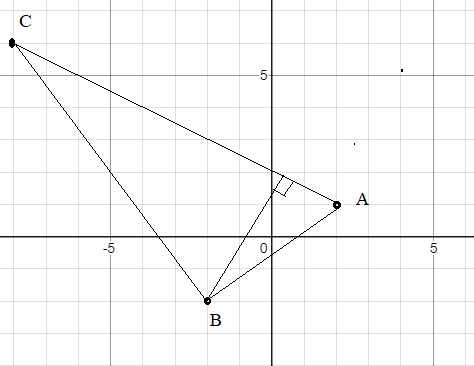
Задача 53702 4.1.23. Даны вершины [m]A(2; 1)[/m],...

5f6a06ffb931bd71f10f35dc

28 сентября 2020 г. в 12:56

4.1.23. Даны вершины [m]A(2; 1)[/m], [m]B(-2; -2)[/m], [m]C(-8; 6)[/m] треугольника [m]ABC[/m]. Найти длину высоты, опущенной из вершины [m]B[/m].

5f3ea7e3faf909182968ddd9

28 сентября 2020 г. в 13:29

★

1 способ
Уравнение прямой АC, как прямой, проходящей через две точки:

x+2y–4=0

Расстояние от точки B до прямой:

d=|(–2)+2·(–2)–4|/√1²+2²=10/√5=2√5

2 cпособ

Уравнение прямой АС, как прямой, проходящей через две точки:

x+2y–4=0

Уравнение прямой, перпендикулярной АС и проходящей через точку В:

y=2x+b
–2=2·(–2)+b
b=2

y=2x+2

Находим координату основания высоты – точки пересечения
x+2y–4=0
и
y=2x+2

K(0; 2)

BK=√(0+2)²+(2–(–2))²=√4+16=√20=2√5