Задача 53629 Задача 3.4. В параллелепипеде [m]ABCD...

5f6c69b5019fbf2dafd19b36

24 сентября 2020 г. в 12:41

Задача 3.4.

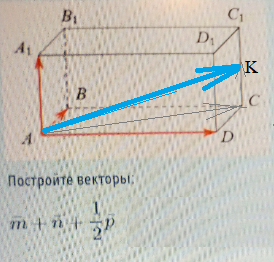
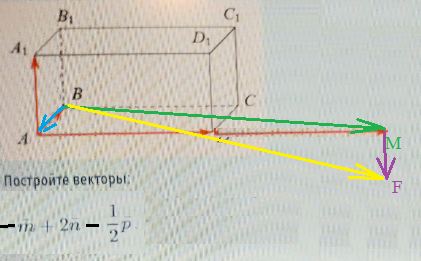
В параллелепипеде [m]ABCD A_1 B_1 C_1 D_1[/m] заданы векторы, совпадающие с его рёбрами: [m]\overrightarrow{AB} = \overrightarrow{m}[/m], [m]\overrightarrow{AD} = \overrightarrow{n}[/m] и [m]\overrightarrow{AA_1} = \overrightarrow{p}[/m].

Постройте векторы:
[m]
\overrightarrow{m} + \overrightarrow{n} + \frac{1}{2} \overrightarrow{p} \quad \text{и} \quad -\overrightarrow{m} + 2\overrightarrow{n} - \frac{1}{2} \overrightarrow{p}.
[/m]

5f3ea7e3faf909182968ddd9

24 сентября 2020 г. в 13:03

★

По правилу параллелограмма:
[m]\vec{AB}+\vec{AD}=\vec{AC}[/m]

[m]\vec{AC}=\vec{m}+\vec{n}[/m]

[m]\vec{AC}+\frac{1}{2}\vec{CC_{1}}=\vec{AC}+\vec{CK}=\vec{m}+\vec{n}+\frac{1}{2}\vec{p}[/m]


[m]\vec{AC}+\vec{CK}=\vec{AK}[/m]


[m]\vec{m}+\vec{n}+\frac{1}{2}\vec{p}=\vec{AK}[/m]


2)

[m]-\vec{m}=\vec{BA}[/m]

[m]2\vec{n}=\vec{AM}[/m]

По правилу треугольника:
[m]-\vec{m}+2\vec{n}=\vec{BA}+\vec{AD}=\vec{BD}[/m]

[m]-\vec{m}+2\vec{n}-\frac{1}{2}\vec{p}=\vec{BA}+\vec{AD}-\frac{1}{2}\vec{AA_{1}}=\vec{BA}+\vec{AD}+\vec{DF}=\vec{BF}[/m]