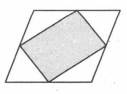
Площадь параллелограмма равна 14. Найдите площадь четырёхугольника, вершинами которого являются середины сторон данного параллелограмма.
математика 10-11 класс
20908
Площадь всего параллелограмма состоит из площади четырех треугольников и площади закрашенного четырехугольника. Площади треугольников будут равны 1/2*1/2 h*1/2 AB, где h – высота параллелограмма и АВ – большая сторона параллелограмма. Четыре таких площади будут равны: 4* 1/8 h*AB= (h*AB)/2. При этом площадь самого параллелограмма равна произведению его высоты на основание. Значит, сумма площадей 4 треугольников равна половине площади всего параллелограмма, т.е. равна 7. Остальную площадь занимает искомый четырехугольник и его площадь равна 14 – 7 = 7.
Ответ: 7
Вопросы к решению (2)
Площади треугольников будут равны 1/2·1/2 h·1/2 AB почему?
есть второй способ решения этой задачи?
Внутренний четырехугольник разделяем на 4 ровные части.И видим, что параллелограмм состоит из 8 похожих треугольников.14:8
=1,75
1,75*4=7(площадь четырехугольника)

