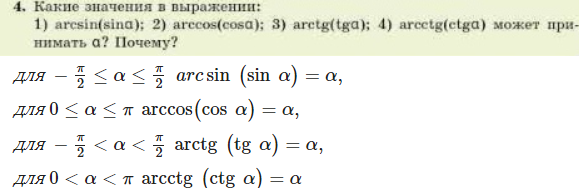Задача 53499 решите пожалуйста...
Условие

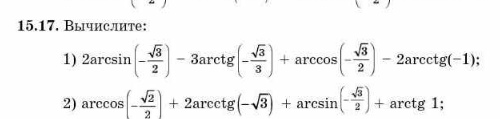


Решение
1)
[m]arccos 0=\frac{\pi}{2}[/m], так как
[m] cos\frac {\pi}{2}=0[/m] и [m]\frac {\pi}{2}\in [0;\pi ][/m]
2)
[m]arccos 1=0[/m], так как
[m] cos0=1[/m] и [m]0\in [0;\pi ][/m]
3)
[m]arccos (-\frac{\sqrt{2}}{2})=\pi-arccos\frac{\sqrt{2}}{2}=\pi-\frac {\pi}{4}=\frac{3 \pi}{4}[/m], так как
[m] cos\frac {\pi}{4}=\frac{\sqrt{2}}{2}[/m] и [m]\frac {\pi}{4}\in [0;\pi ][/m]
и
[m] cos\frac {3\pi}{4}=-\frac{\sqrt{2}}{2}[/m] и [m]\frac {3\pi}{4}\in [0;\pi ][/m]
4)
[m]arccos (-\frac{\sqrt{3}}{2})=\pi-arccos\frac{\sqrt{3}}{2}=\pi-\frac {\pi}{6}=\frac{5 \pi}{6}[/m], так как
[m] cos\frac {\pi}{6}=\frac{\sqrt{3}}{2}[/m] и [m]\frac {\pi}{6}\in [0;\pi ][/m]
и
[m] cos\frac {5\pi}{6}=-\frac{\sqrt{3}}{2}[/m] и [m]\frac {5\pi}{6}\in [0;\pi ][/m]
15.8
1)
[m] arctg 1=\frac {\pi}{4}[/m], так как
[m] tg\frac {\pi}{4}=1[/m] и [m]\frac {\pi}{4}\in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
2)
[m] arctg 0=0[/m], так как
[m] tg0=0[/m] и [m]0 \in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
3)
[m] arctg (-1)=-\frac {\pi}{4}[/m], так как
[m] tg(-\frac {\pi}{4})=-1[/m] и [m]-\frac {\pi}{4}\in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
4)
[m] arctg (-\frac{\sqrt{3}}{3})=-\frac {\pi}{6}[/m], так как
[m] tg(-\frac {\pi}{6})=-\frac{\sqrt{3}}{3}[/m] и [m]-\frac {\pi}{6}\in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
15.4
1)
[m]arccos (-\frac{\sqrt{2}}{2})+arcsin(-\frac{1}{2})=\frac{3 \pi}{4}+(-\frac {\pi}{6})=-\frac {7 \pi}{12}[/m]
Так как
[m]arccos (-\frac{\sqrt{2}}{2})=\pi - arccos\frac{\sqrt{2}}{2}=\pi-\frac {\pi}{4}=\frac{3 \pi}{4}[/m],
[m] cos\frac {3\pi}{4}=-\frac{\sqrt{2}}{2}[/m] и [m]\frac {3\pi}{4}\in [0;\pi ][/m]
[m]arcsin(-\frac{1}{2})=-\frac {\pi}{6}[/m],
[m] sin(-\frac {\pi}{6})=-\frac{1}{2}[/m] и [m]-\frac {\pi}{6}\in [-\frac {\pi}{2};\frac {\pi}{2}][/m]
2)
[m]arccos (-\frac{\sqrt{3}}{2})-arcsin(\frac{\sqrt{3}}{2})=\frac{5 \pi}{6}-\frac {\pi}{3}=\frac { \pi}{2}[/m]
3)
[m]arccos(0,5)+arcsin(-1)=\frac{\pi}{3}-\frac {\pi}{2}=-\frac { \pi}{6}[/m]
4)
[m]arccos (\frac{\sqrt{3}}{2})-arcsin(-\frac{\sqrt{2}}{2})=\frac{ \pi}{6}-(-\frac {\pi}{4})=\frac { 5\pi}{12}[/m]
15.17
1)
[m]2arcsin \frac{\sqrt{3}}{2}-3arctg(-\frac{\sqrt{3}}{3})+arccos (-\frac{\sqrt{3}}{2})-2arctg(-1)=2\cdot \frac { \pi}{6} -3\cdot (-\frac { \pi}{6})+\frac{5 \pi}{6}-2\cdot (-\frac{ \pi}{4})=[/m]
[m]=\frac{13 \pi}{6}[/m]
2)
[m]arccos (-\frac{\sqrt{2}}{2})+2arctg(-\sqrt{3}+arcsin (-\frac{\sqrt{3}}{2})+arctg1= -\frac {3 \pi}{4}+2\cdot (-\frac {\pi}{3})+(-\frac {\pi}{3})+\frac {\pi}{4}=-\frac{3 \pi}{2}[/m]