Задача 5334 В правильной четырёхугольной пирамиде...
Условие
а) Пусть О — центр основания пирамиды. Докажите, что прямые ВО и LO перпендикулярны.
б) Найдите площадь поверхности пирамиды.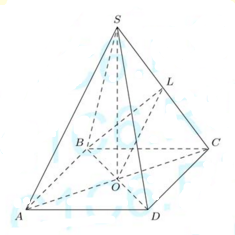
Решение
Диагонали к на л para пересекаются под прямым углом, поэтому ВО±АС. С другой сто|К)ны SO - высота пирамиды и BOLSO. Следовательно, прямая ВО перпендикулярна плоскости ACS, в частности BOLLO. Таким образом, треугольник BLO прямоугольный:
tg<BLO = BO/LO; BO = BD/2 = (sqrt(AB^2+AD^2))/2 = 4sqrt(2);
LO = BO/tg<BLO; LO = 4sqrt(2)/2sqrt(2/5) = 2sqrt(5); SA = 4sqrt(5).
Площадь боковой грани можно найти по формуле Герона:
p = (AB+SA+SB)/2 = 4+4sqrt(5); S(ABS) = sqrt(p(p-AB)(p-SA)(p-SB)) = sqrt(((4sqrt(5)+4)(4sqrt(5)-4)*4*4) = 32.
Площадь поверхности пирамиды равна: S = S(ABCD) + 4S(ABS) = 64+4*32 = 192.
Ответ: 192