Задача 532 Найдите все значения а, при каждом из...

slava191

29.01.2014

Найдите все значения а, при каждом из которых наибольшее значение функции f(x)=x^2-7|x-a|-3x на отрезке [-6;6] принимает хотя бы на одном из концов этого отрезка.

Для начала прикинем, как ведет себя функция на этом отрезке при изменении параметра a:

При x>a: f(x) = f1(x) = x^2-10x+7a
При x<a: f(x) = f2(x) = x^2+4x-7a
При x=a: f(x) = x^2-3x = a^2-3a

Функция может достигать максимального значения либо на границах отрезка, либо в точках максимума (если они есть), либо в особой точке (где выражение под модулем меняет свой знак, т.е. при x=a).

f1'(x) = (x^2-10x+7a)' = 2x-10. Экстремум в точке x=5, и это точка минимума (производная меняет знак с отрицательного на положительный).
f2'(x) = (x^2+4x-7a)' = 2x+4. Экстремум в точке x=-2, и это тоже точка минимума.
Так что максимумов у функции нет. Следовательно, наибольшего значения функция f(x) может достичь только либо на одной из границ отрезка [-6;6], либо в точке x=a.

Если a < -6 или a > 6, то функция всегда принимает максимальное значение на одной из границ отрезка, поскольку особая точка лежит вне его.

Если a принадлежит [-6;6], то условие выполняется, когда справедливо хотя бы одно из неравенств:

(1): f2(-6)>=f(a) (значение функции в левой границе отрезка больше ее значения в особой точке)
(2): f1(6)>=f(a) (значение функции в правой границе отрезка больше ее значения в особой точке)

(1): 36-24-7a >= a^2-3a
a^2+4a-12 <= 0
a принадлежит [-6;2]

(2): 36-60+7a >= a^2-3a
a^2-10a+24 <=0
a принадлежит [4;6]

Таким образом, функция f(x) принимает своё наибольшее значение на отрезке [-6;6] при всех значениях a от минус бесконечности до 2 включительно и от 4 включительно до плюс бесконечности.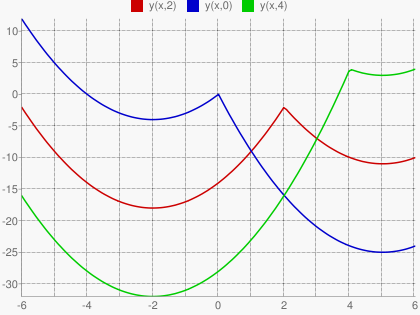

Ответ: a ? (–?;2]?[4;+?)