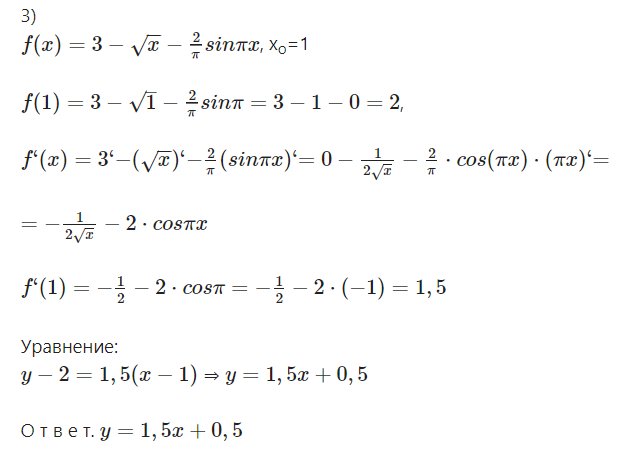Задача 53109 Номер 11 все ...
Условие
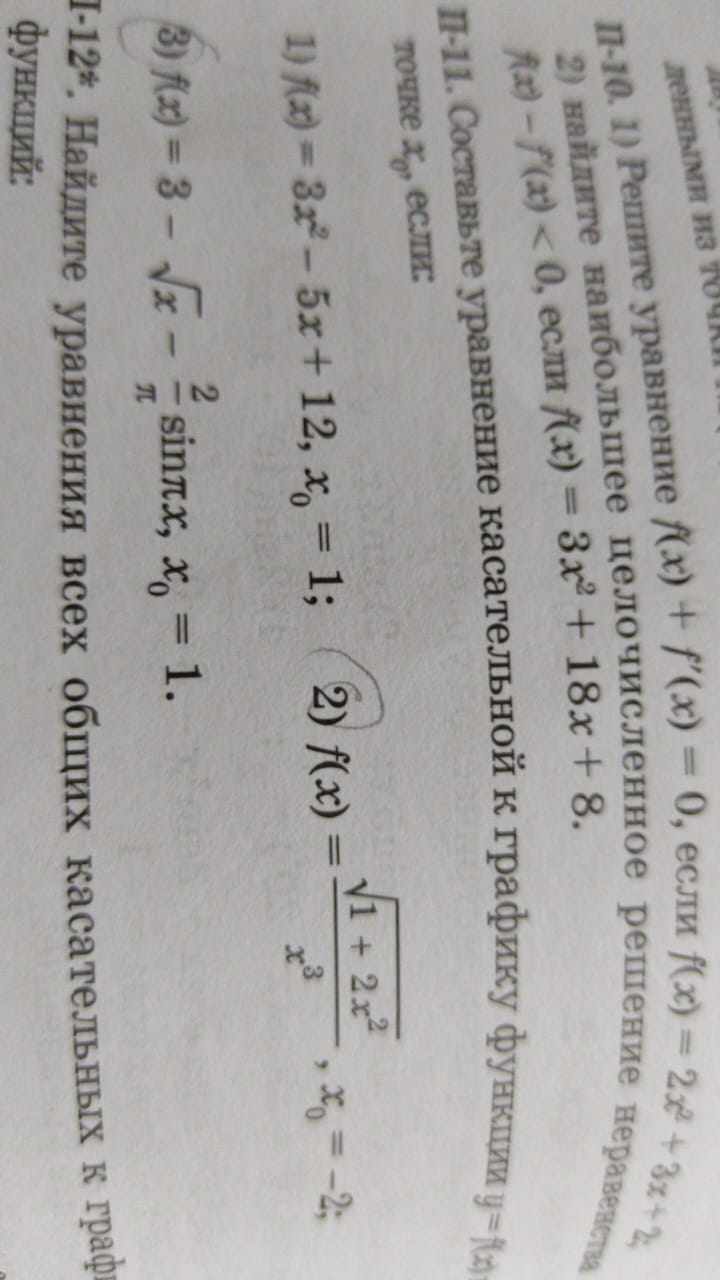
Решение
y - f(x_(o)) = f `(x_(o)) * ( x - x_(o))
[b]1) [/b]
f(x)=3x^2-5x+12, x_(o)=1
f(x_(o))=f(1)=3*1^2-5*1+12=10
f ` ( x) = (3x^2-5x+12)` =6x-5
f `(x_(o))=f`(1)=6*1-5=1
y - 10 = 1*(x-1) ⇒ [b]y=x+9 - уравнение касательной[/b]
О т в е т. [b]y=x+9 [/b]
[b]2)[/b]
[m]f(x)=\frac{\sqrt{1+2x^2}}{x^3}[/m], x_(o)=-2
[m] f(x_{o})=\frac{\sqrt{1+2\cdot (-2)^2}}{(-2)^3}=-\frac{3}{8}[/m]
[m]f`(x)=\frac{(\sqrt{1+2x^2})`\cdot x^3-\sqrt{1+2x^2}\cdot (x^3)`}{(x^3)^2}=[/m]
[m]=\frac{\frac{1}{2\sqrt{1+2x^2}}\cdot (1+2x^2)``\cdot x^3-\sqrt{1+2x^2}\cdot (3x^2)}{x^6}=[/m]
[m]=\frac{2x^4-3x^2\cdot(1+2x^2)}{\sqrt{1+2x^2}\cdot x^6}=\frac{-4x^2-3}{\sqrt{1+2x^2}\cdot x^4}[/m]
[m]f`(-2)=-\frac{19}{48}[/m]
[m]y-(-\frac{3}{8})=-\frac{19}{48}\cdot (x-(-2))[/m]
[m] y=-\frac{19}{48}\cdot x-\frac{56}{48} [/m]- уравнение касательной
О т в е т. [m] y=-\frac{19}{48}\cdot x-\frac{56}{48} [/m]
