Задача 52962 ...
Условие
(|x| - 5)^2 + (y - 4)^2 = (2 - |x|/x)^2.
Среди всех прямых, касающихся этой кривой в двух точках, найдите ту прямую, которая наименее удалена от точки с координатами (10 - 4√6; 6).
Решение
|x|=x
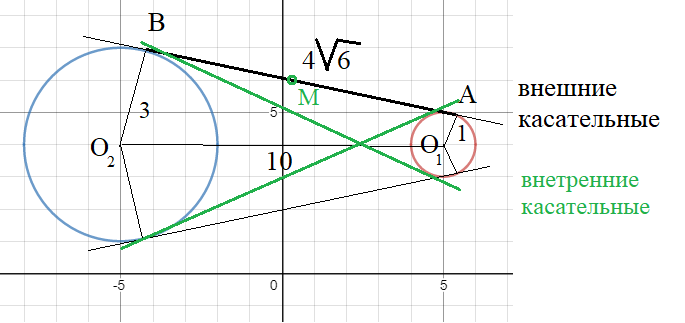
Получаем окружность:[b] (x-5)^2+(y-4)^2=1^2[/b]
При x < 0
|x|=-x
Получаем окружность: (-x-5)^2+(y-4)^2=3^2 ⇒[b] (x+5)^2+(y-4)^2=3^2[/b]
см. рис.
Пусть А (x_(1);y_(1)) принадлежит первой окружности:
(x_(1)-5)^2+(y_(1)-4)^2=1^2
В (x_(2);y_(2)) принадлежит второй окружности:
[b] (x_(2)+5)^2+(y_(2)-4)^2=3^2
Составим уравнения прямой О_(1)А
[m]\frac{x-5}{x_{1}-5}=\frac{y-4}{y_{1}-4}[/m]
и прямой О_(2)В
[m]\frac{x+5}{x_{2}+5}=\frac{y-4}{y_{2}-4}[/m]
Прямые параллельны, значит их угловые коэффициенты равны.
[m]\frac{y_{2}-4}{x_{2}+5}=\frac{y_{1}-4}{x_{1}-5}[/m]
Получаем систему уравнений:
{(x_(1)-5)^2+(y_(1)-4)^2=1^2
{(x_(2)+5)^2+(y_(2)-4)^2=3^2
{[m]\frac{y_{2}-4}{x_{2}+5}=\frac{y_{1}-4}{x_{1}-5}[/m]
Находим координаты точек А и В
Составляем уравнение касательной АВ.
Касательная АВ расположена ближе всех к точке М