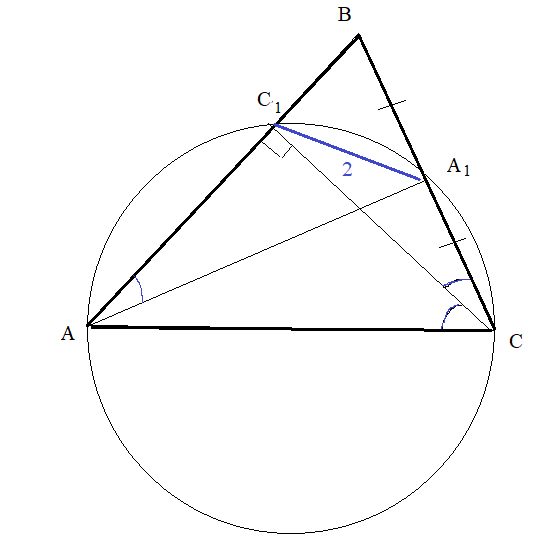
Задача 52944 В остроугольном треугольнике АВС...

slava191

31 июля 2020 г. в 22:27

В остроугольном треугольнике АВС проведены высота СС1, и медиана AA1, причём точки А, С, A1 и С1, лежат на одной окружности.

а) Докажите, что треугольник АВС равнобедренный.

б) Найдите площадь треугольника АВС, если АА1 :СС1, =3:2 и А1С1 = 2.

sova

1 августа 2020 г. в 11:54

★

а)
CC₁ ⊥ AB ⇒ ∠ AC₁C=90 °

∠ AA₁C= ∠ AC₁C=90 ° как углы опирающиеся на одну и ту же дугу АС

AA₁ ⊥ BC
Медиана AA₁ одновременно и высота, значит Δ АВС – равнобедренный
АВ=АС

б) АВ=АС
A₁C₁=2

[m]\angle C_{1}AA_{1}=\angle A_{1}CC_{1}[/m] как углы,

опирающиеся на одну и ту же дугу A₁C₁

Δ АА₁В= Δ АА₁С ⇒ ∠ АА₁В= ∠ АА₁С ⇒ ∪ А₁С= ∪ А₁С₁=2

A₁C=2

BC=4


Пусть АА₁=3х; СС₁=2х

Из Δ ВС₁С:

[m] sin \angle B=\frac{CC_{1}}{BC}=\frac{x}{2}[/m]

[m] sin \angle C= sin \angle B=\frac{x}{2}[/m]

Из Δ AС₁С:

[m] sin \angle C=\frac{CC_{1}}{AC}=\frac{3x}{AC}[/m] ⇒

[m]\frac{x}{2}=\frac{3x}{AC}[/m] ⇒ АС=6; BC=6

Из Δ АА₁С:

[m]AA_(1)=\sqrt{AC^2-CA^2_{1}}=\sqrt{36-4}=\sqrt{32}=4\sqrt{2}[/m]

S _{Δ ABC}=[m]\frac{1}{2}BC\cdot AA_{1}=2\cdot 4\sqrt{2}=8\sqrt{2}[/m]

О т в е т. [m]8\sqrt{2}[/m]