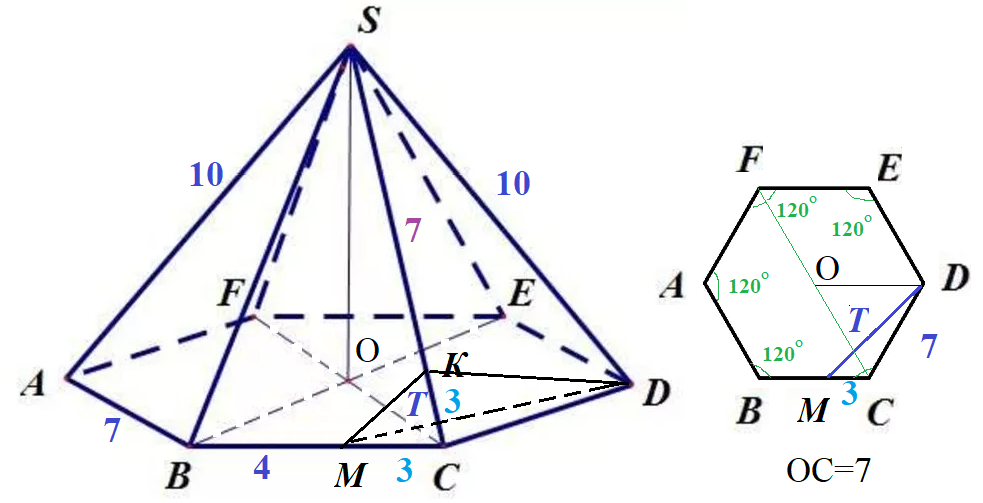
Задача 52943 В правильной шестиугольной пирамиде...

slava191

2020-07-31 22:27:31

В правильной шестиугольной пирамиде SABCDEF сторона основания АВ равна 7, а боковое ребро SA равно 10. На рёбрах ВС и SC отмечены точки М и К соответственно, причём ВМ = 4, SK = 7.

а) Докажите, что плоскость MKD перпендикулярна плоскости АВС.

б) Найдите объём пирамиды CDKM .

sova

2020-08-01 12:32:16

★

Пирамида правильная:

В основании правильный шестиугольник:
AB=BC=CD=DE=DF=AD=7

Боковые ребра равны: SA=SB=SC=SD=SE=SF=10

ОС=ОD=7

Δ OTD ∼ Δ MTC
3 : 7=ТС: (7-ТС) ⇒ 7ТС=21-3ТС ⇒ [b]ТС=2,1[/b]

Покажем, что Т- проекция точки K

Рассмотрим Δ SOC и Δ KTC
∠ SСО - общий.

SO:KO= 10:3
OC:ТС=7:2,1=10:3 ⇒ Δ SOC подобен Δ KTC

∠ SOC=90 ° ⇒ ∠ KTC=90 °

б)
По теореме Пифагора

KT^2=KC^2-CТ^2=3^2-2,1^2=0,9*5,1

КT=3sqrt(51)/10

V_(пирамиды СDKM)=(1/3)*S_( Δ CDM)*H=

=(1/3)*(1/2)*CМ*МD*sin120 °*KT=(1/6)*3*7*(sqrt(3)/2)*(3sqrt(51)/10)=

=[b]63sqrt(17)/40[/b]