Задача 52942 ...

slava191

2020-07-31 22:09:03

Верхняя грань АВ прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина α = 30°. Луч света падает из воздуха на клин перпендикулярно грани АС, преломляется и выходит в воздух через другую грань под углом γ= 45° к её нормали. Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

Поскольку луч падает на грань АС перпендикулярно, он на ней не преломляется, а, падая на грань АВ, согласно закону отражения света отражается под тем же углом α. Следовательно, так как KN || ВС, то β = 90 - 2α.
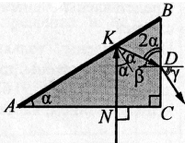
Закон преломления света в точке D: n sinβ = sinγ, nsin(90-2α) = sinγ.
Получаем: п = sinγ/cos2α ≈1,4.
Ответ: п = 1,4