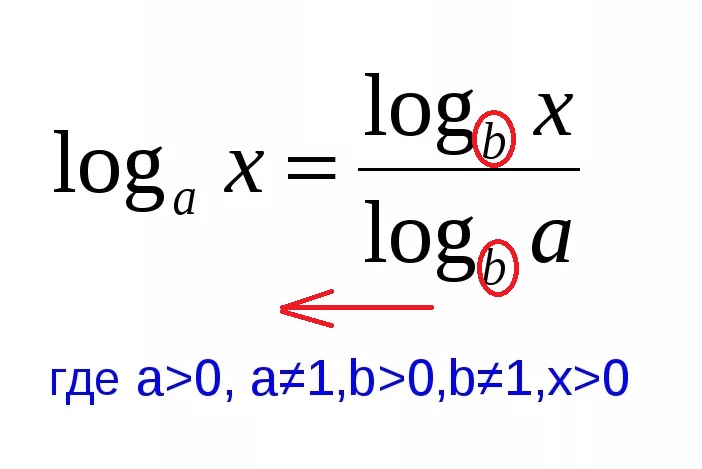Задача 52930 Решите уравнение log_(1/2) (x+2) · log_7...

wolandzilber

29 июля 2020 г. в 16:01

Решите уравнение log_1/2 (x+2) · log₇ (x+2) = –log₇ 2

sova

29 июля 2020 г. в 16:11

★

ОДЗ:
x+2 > 0 ⇒ x > –2

Делим обе части уравнения на
[m] -log_{7} 2=log_{7}2^{-1}=log_{7}\frac{1}{2}[/m]

и применяем формулу перехода к другому основанию справа налево:

[m]\frac{log_{\frac{1}{2}}(x+2)\cdot log_{7}(x+2)}{log_{7}\frac{1}{2}}=1[/m]

[m]log_{\frac{1}{2}}(x+2)\cdot log_{\frac{1}{2}}(x+2)=1[/m]

[m]log^2_{\frac{1}{2}}(x+2)=1[/m] ⇒

[m]log_{\frac{1}{2}}(x+2)=-1[/m] или [m]log_{\frac{1}{2}}(x+2)=1[/m]

По определению:

[m] x+2=(\frac{1}{2})^{-1}[/m] или [m] x+2=(\frac{1}{2})^{1}[/m]

[m] x+2=2[/m] или [m] x+2=\frac{1}{2}[/m]

[m] x=0[/m] или [m] x=-2+\frac{1}{2}=-1,5[/m]

Оба корня входя в ОДЗ

О т в е т. –1,5; 0