Задача 52915 помогите решить неравенство...
Условие
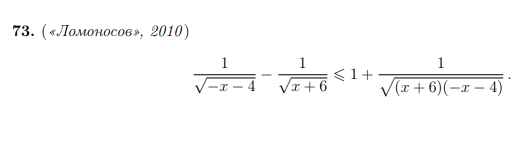
Решение

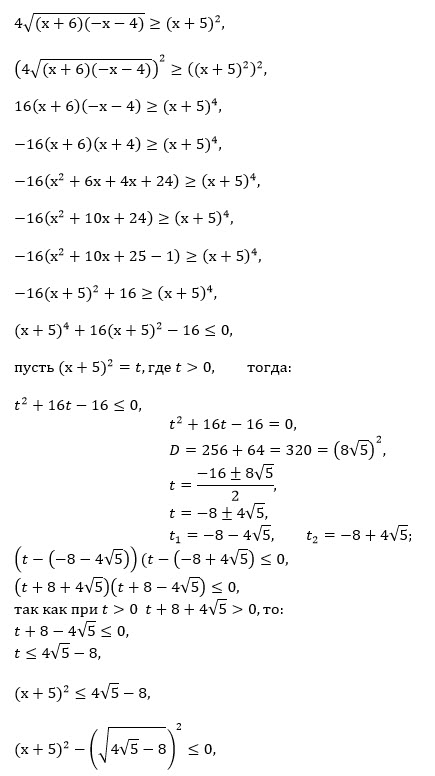

Все решения
[m]\left\{\begin{matrix} x+6 >0\\ -x-4 >0 \end{matrix}\right.[/m]
[red]x ∈ (-6;-4)[/red]
[m]\frac{1}{\sqrt{-x-4}}-\frac{1}{\sqrt{x+6}}\leq 1+\frac{1}{\sqrt{(x+6)(-x-4)}}[/m]
Перепишем неравенство в виде:
[m] 1+\frac{1}{\sqrt{(x+6)(-x-4)}}\geq\frac{1}{\sqrt{-x-4}}-\frac{1}{\sqrt{x+6}}[/m]
Получили неравенство вида: f(x) ≥ g(x)
Так как
[m]1+\frac{1}{\sqrt{(x+6)(-x-4)}}\geq 0[/m] при [red]x ∈ (-6;-4)[/red]
то рассматриваем два случая:
1)
Если [m] \frac{1}{\sqrt{-x-4}}-\frac{1}{\sqrt{x+6}} ≤ 0[/m],
то неравенство верно при любых [red]x ∈ (-6;-4)[/red]
[m] \frac{1}{\sqrt{-x-4}}-\frac{1}{\sqrt{x+6}} ≤ 0[/m] ⇒ [m]\sqrt{x+6} ≤ \sqrt{-x-4}[/m]
⇒ x+6 ≤ -x-4 ⇒ 2x ≤ -10; x ≤ -5
Ответ первого случая [b](-6;-5][/b]
2)
Если [m] \frac{1}{\sqrt{-x-4}}-\frac{1}{\sqrt{x+6}} > 0[/m], т.е [blue] x >-5[/blue]
Левая и правая части неотрицательны, [i]возводим[/i] неравенство [i]в квадрат[/i]:
[m] (1+\frac{1}{\sqrt{(x+6)(-x-4)}})^2\geq(\frac{1}{\sqrt{-x-4}}-\frac{1}{\sqrt{x+6}})^2[/m]
[m] 1+\frac{2}{\sqrt{(x+6)(-x-4)}}+ \frac{1}{(x+6)(-x-4)}\geq \frac{1}{-x-4}-\frac{2}{\sqrt{(x+6)(-x-4)}}+\frac{1}{x+6}[/m]
[m]\frac{4}{\sqrt{(x+6)(-x-4)}}\geq (\frac{1}{x+6}-1) -\frac{1}{-x-4}\cdot (\frac{1}{x+6}-1)[/m]
[m]\frac{4}{\sqrt{(x+6)(-x-4)}}\geq (\frac{1}{x+6}-1)\cdot (1 -\frac{1}{-x-4})[/m]
[m]\frac{4}{\sqrt{(x+6)(-x-4)}}\geq \frac{1-x-6}{x+6}\cdot (\frac{-x-4-1}{-x-4})[/m]
[m]\frac{4}{\sqrt{(x+6)(-x-4)}}\geq \frac{(-x-5)^2}{(x+6)(-x-4)}[/m]
Возводим в квадрат:
[m]\frac{16}{(x+6)(-x-4)}\geq \frac{(-x-5)^4}{(x+6)^2(-x-4)^2}[/m]
[m](-x-5)^{4}\leq16(x+6)(-x-4)[/m]
[i]Замена переменной:[/i]
-x-5=t ⇒ x=-t-5
x+6=-t-5+6=-t+1
-x-4=-(-t-5)-4=t+1
[m]t^{4}\leq16(-t+1)(t+1)[/m]
[m]t^{4}+16t^2-16\leq0[/m]
D=256+64=320=(64*5)
[m]t_{1}^2=\frac{-16+8\sqrt{5}}{2}=-8+4\sqrt{5} >0 [/m]
[m]t_{2}^2=\frac{-16-8\sqrt{3}}{2}=-8-4\sqrt{5} <0 [/m]
⇒ [m] (t^2-(-8+4\sqrt{5}))\cdot (t^2-(-8-4\sqrt{5})\leq0[/m]
так как [m]t^2-(-8-4\sqrt{5} \geq0[/m], то
[m]t^2\leq 4\sqrt{3}-8[/m] ⇒ [m] - \sqrt{4\sqrt{5}-8}\leq t \leq \sqrt{4\sqrt{5}-8}[/m] ⇒
[m] - \sqrt{4\sqrt{5}-8}\leq -x-5 \leq \sqrt{4\sqrt{5}-8}[/m] ⇒
[m] - \sqrt{4\sqrt{5}-8}+5 \leq -x \leq \sqrt{4\sqrt{5}-8}+5[/m] ⇒
[m] -\sqrt{4\sqrt{5}-8}-5 \leq x \leq \sqrt{4\sqrt{5}-8}-5[/m]
C учетом условия второго случая x > -5
получаем: [m](-5; \sqrt{4\sqrt{5}-8}-5][/m]
О т в е т.[m] (-6;-5][/m] U [m](-5; \sqrt{4\sqrt{5}-8}-5] =(-6; \sqrt{4\sqrt{5}-8}-5][/m]
