Задача 52885 При каких значениях x график функции y= ...

wolandzilber

20 июля 2020 г. в 17:46

При каких значениях x график функции y= |(2x+3)/(x–2)|–2 расположен выше оси Ox?

sova

20 июля 2020 г. в 19:27

Чтобы ответить на вопрос при каких значениях

[m]y=|\frac{2x+3}{x-2}|-2[/m] расположен выше оси Ох, надо решить

неравенство

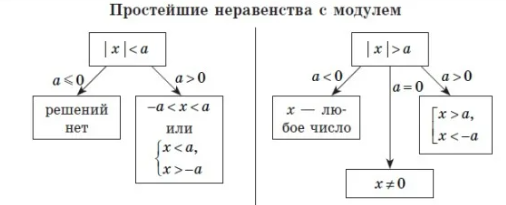
[m]|\frac{2x+3}{x-2}|-2>0[/m] или [m]|\frac{2x+3}{x-2}|>2[/m], которое

равносильно совокупности неравенств ( см приложение):

[m]\frac{2x+3}{x-2}< -2 [/m] или [m]\frac{2x+3}{x-2}>2[/m]

[m]\frac{2x+3}{x-2}+2< 0 [/m] или [m]\frac{2x+3}{x-2}-2>0[/m]

[m]\frac{2x+3+2x-4}{x-2}< 0 [/m] или [m]\frac{2x+3-2x+4}{x-2}>0[/m]

[m]\frac{4x-1}{x-2}< 0 [/m] или [m]\frac{7}{x-2}>0[/m] ⇒ x–2 >0; x>2

Решаем первое методом интервалов:

_+__ ([m]\frac{1}{4}[/m]) __–__ (2) _+__

О т в е т. ([m]\frac{1}{4}[/m];2)U(2;+ ∞ )