Задача 52882 ...

look

2020-07-19 23:08:57

В правильной шестиугольной пирамиде SABCDEF угол между прямыми SA и BC равен π/3. Найдите угол между плоскостями: 1) SCD и SEF; 2) SAB и SDE.

sova

2020-07-20 11:07:29

BC|| АО ⇒ угол между прямыми SA и BC равен углу между

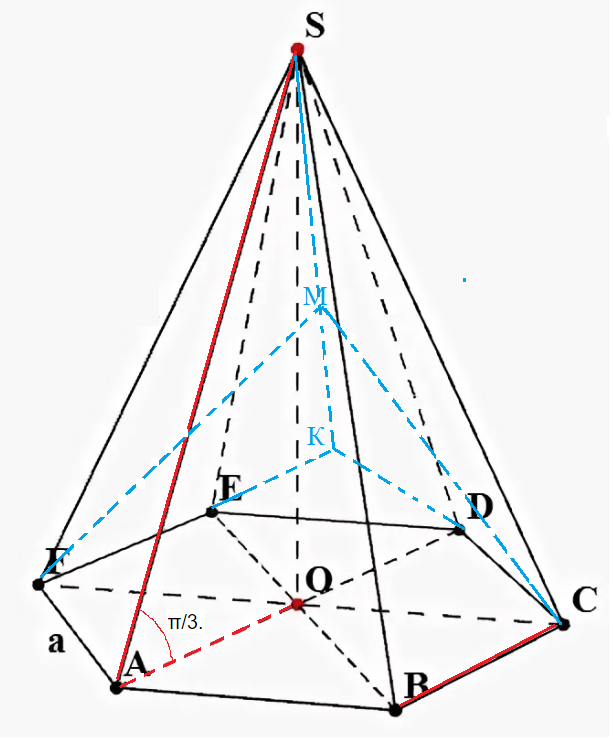
прямыми SA и AO ⇒ ∠ SAO=π/3

Пирамида правильная ⇒
∠ SAO= ∠ SBO= ∠ SCO= ∠ SDO= ∠ SFO= ∠ SEO=π/3 ⇒

Δ SAD и Δ SFC и Δ SBE - равносторонние.

⇒ SA=SB=SB=SC=SD=SF=SE=2AD=2AB=[b]2a[/b], [b]а[/b]- сторона основания шестиугольника

a)
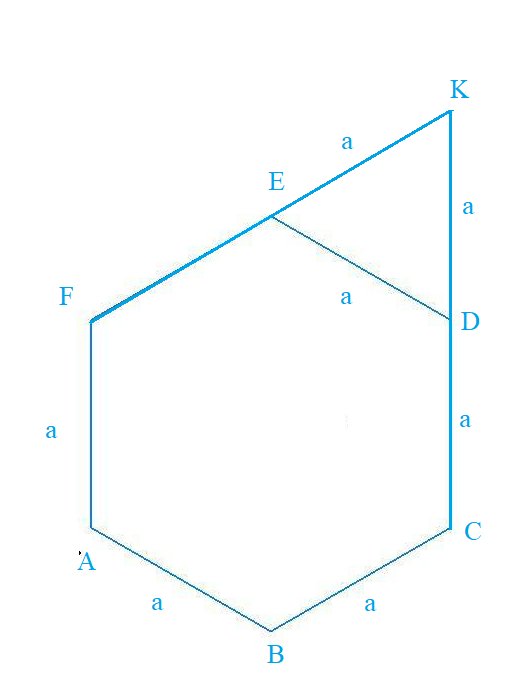
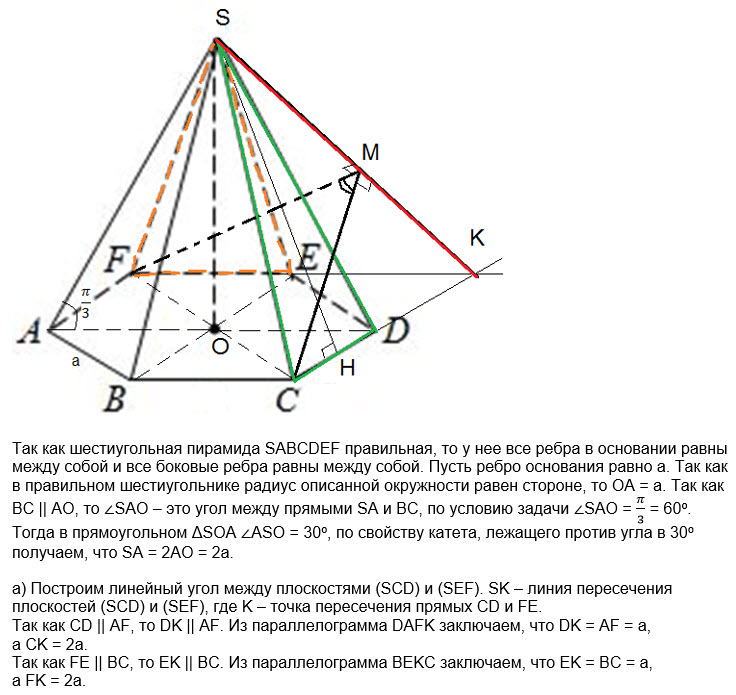
пл. SCD и пл. SEF пересекаются по прямой SK
K- точка пересечения прямых CD и EF ( см. рис.2)

Δ ЕКD - равносторонний.

[b]FК= 2а
СК=2a[/b]

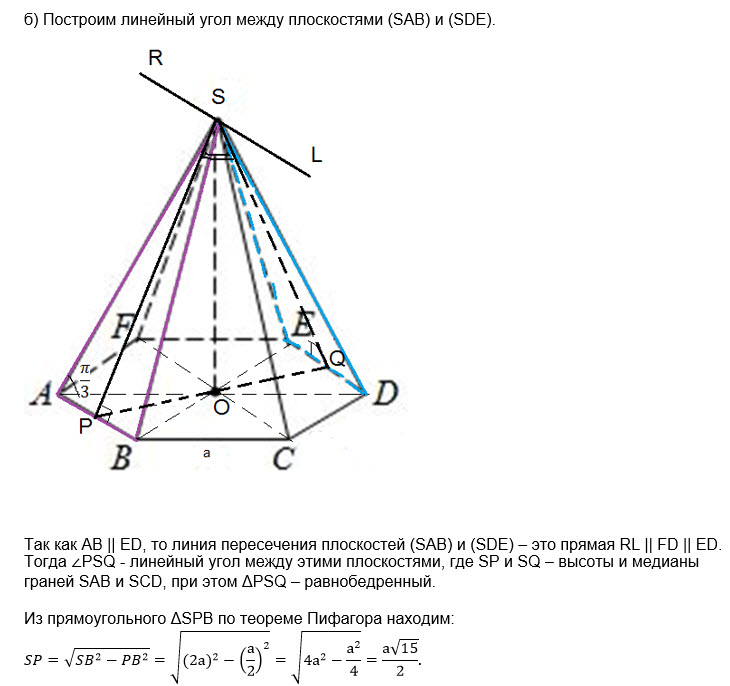
Чтобы найти угол между плоскостями, проводим перпендикуляры
к линии их пересечения.

CM ⊥ SK
FM ⊥ SK

∠ СМF- искомый.

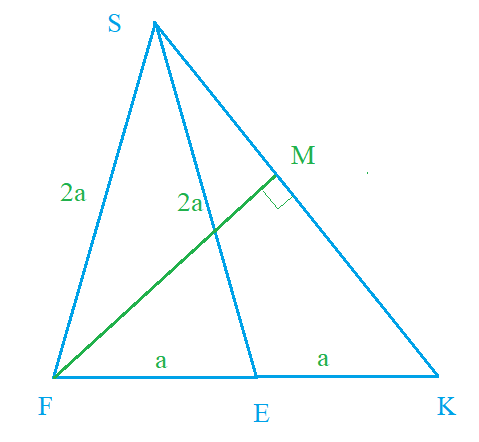
Рассматриваем Δ SFK (рис.3):
SF=SE=[b]2a[/b]
FE=EK=[b]a[/b]

Находим SK из Δ SFK методом удвоения медианы SE
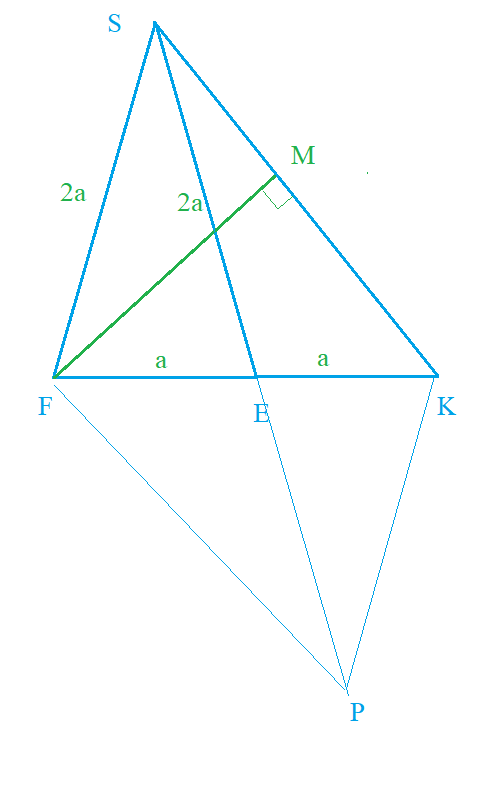
Продолжим медиану SE за точку E на длину [b]2a[/b]

Получим параллелограмм FSKP (рис.4)

По формуле, связывающей стороны и диагонали параллелограмма:
2*(a^2+b^2)=d^2_(1)+d^2_(2)

получим равенство:
2*((2а)^2+SK^2)=(4a)^2+(2a)^2 ⇒ 2SK^2=12a^2 ⇒ SK^2=6a^2

SK=[b]a sqrt(6)[/b]

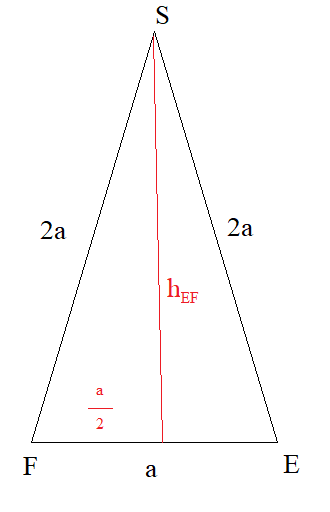
Из Δ SEF:
SF=2a; SE=2a; EF=a

cos ∠ F=cos ∠ E=[m]\frac{\frac{a}{2}}{2a}=\frac{1}{4}[/m]

sin ∠ F=sin ∠ E=sqrt{1-(1/4)^2)=sqrt(15)/4

Тогда h_(FE)=SF*sin ∠ F=2a*(sqrt(15)/4)=[b](a/2)*sqrt(15)[/b]

В Δ SFK

h_(FK)=h_(FE)=[b](a/2)*sqrt(15)[/b]

S_( ΔSFK)=(1/2) FK*h_(FK)

S_( ΔSFK)=(1/2) SK*FM ⇒ SK*FM=FK*h_(FK) ⇒ asqrt(6)*FM==2a*[b](a/2)*sqrt(15)[/b]

FM=2a*[b](a/2)*sqrt(15)[/b]/a sqrt(6)=[b]a*sqrt(5/2)[/b]

Аналогично,
CM=[b]a*sqrt(5/2)[/b]

Из Δ FMC по теореме косинусов:

FC^2=FM^2+CM^2-2FM*CM*cos∠ СМF ⇒


cos∠ СМF=[m]\frac{\frac{5a^2}{2}+\frac{5a^2}{2}-4a^2}{2\cdot a \sqrt{\frac{5}{2}}\cdot a\sqrt{\frac{5}{2}}}=[/m]

[m]=\frac{1}{5}[/m] ⇒

∠ СМF=[m]arccos\frac{1}{5}[/m]