Задача 5287 В треугольнике ABC AC = BC, AB = 2, sinA...
Условие
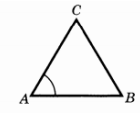
математика 10-11 класс
36191
Решение
AC=CH/sinA по определению синуса
AC= sqrt(CH^2+AH^2) по теореме Пифагора
Можно приравнять левые части уравнений и найти СН:
CH/sinA= sqrt(CH^2+AH^2 )
Возведем обе части в квадрат и перемножим крайние и средние члены пропорции:
16CH/15=CH^2+1
16CH^2=15CH^2+15
CH^2=15
CH= sqrt(15)
Подставим это значение в первую формулу и найдем АС:
AC=(4*sqrt(15))/sqrt(15) = 4
Ответ: 4