Задача 52849 2sin^2(Pi/2-x)+sin2x = 0, [3Pi; 9Pi/2]...
Условие
математика 10-11 класс
63502
Решение
★
sin(π/2–x)=cosx
Уравнение принимает вид:
2cos^2x+sin2x=0
Так как sin2x=2sinx*cosx, то
2cos^2x+2sinx*cosx=0
2cosx*(cosx+sinx)=0
Произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0:
cosx=0 или cosx+sinx=0
[b]x=(π/2)+πn, n ∈ Z[/b] или sinx=-cosx; tgx=-1 ⇒[b] x=-(π/4)+πk, k ∈ Z[/b]
О т в е т.
a) [b](π/2)+πn, n ∈ Z[/b] ; [b] x=-(π/4)+πk, k ∈ Z[/b]
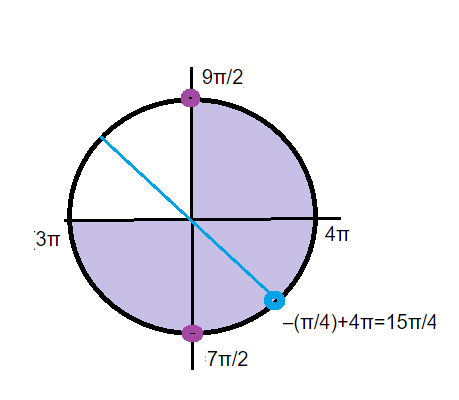
б) x=7π/2; x=9π/2; x=-(π/4)+4π=15π/4- корни,
принадлежащие отрезку [3π; 9π/2]