Задача 52813 ...

tupiza

2020-07-02 18:12:17

Найдите все значения параметра a, при которых система уравнений

x^(2)+y^(2)=a
sin(πx+πy)=0

имеет ровно четыре решения.

sova

2020-07-02 18:59:08

sin(πx+πy)=0 ⇒ πx+πy=πk, k ∈ Z ⇒ x+y=k, k ∈ Z


Решаем систему способом подстановки: y=k-x

x^2+(k-x)^2=a ⇒ 2x^2-2kx+k^2-a=0

D=(-2k)^2-4*2*(k^2-a)=4k^2-8k^2+8a=8a-4k^2

D>0 квадратное уравнение имеет два корня:

2a-k^2>0 ⇒ [b]a>k^2/2[/b]


k= ± 1 ⇒ [red]a>1/2[/red]

{x+y=1
{x^2+y^2=a

или

{x+y=-1
{x^2+y^2=a

получим [red]4 решения
[/red]


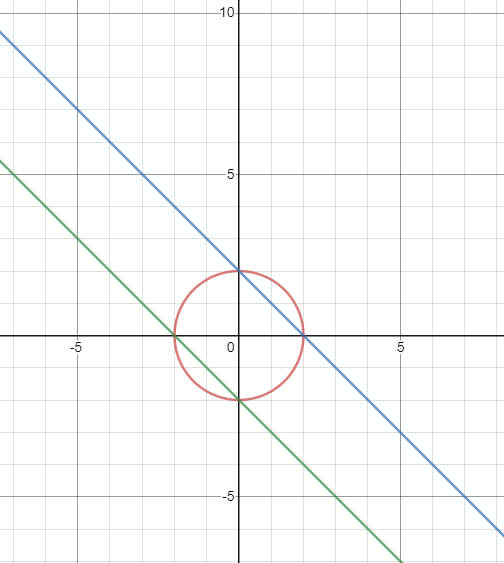
Графическая интерпретация:
Прямые x+y= ± k (k ≠ 0) не должны являться касательными к окружности x^2+y^2=a

т.е. [b]a ≠ k^2/2; k - целое; k ≠ 0[/b]