Задача 52762 Найдите все значения a, при каждом из...

tupiza

2020-06-28 16:33:35

Найдите все значения a, при каждом из которых наименьшее значение функции

f(x)=x-2|x|+|x^(2)-2(a+1)x+a^(2)+2a|

больше 4?

sova

2020-06-28 20:07:44

x^2-2(a+1)+a^2+2a=(x-(a+1))^2-1=(x-a-2)(x-а)

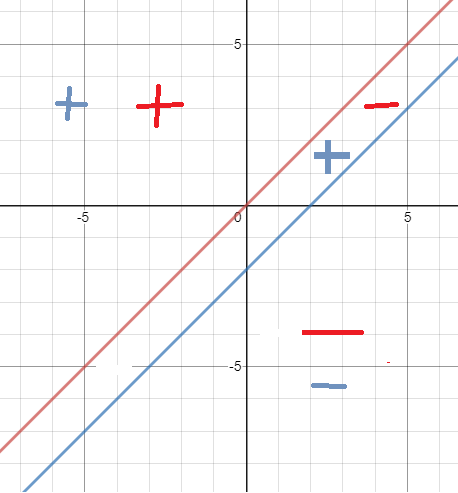
Рассматриваем координатную плоскость хОа:
(далее рассуждения аналогичны методу интервалов)

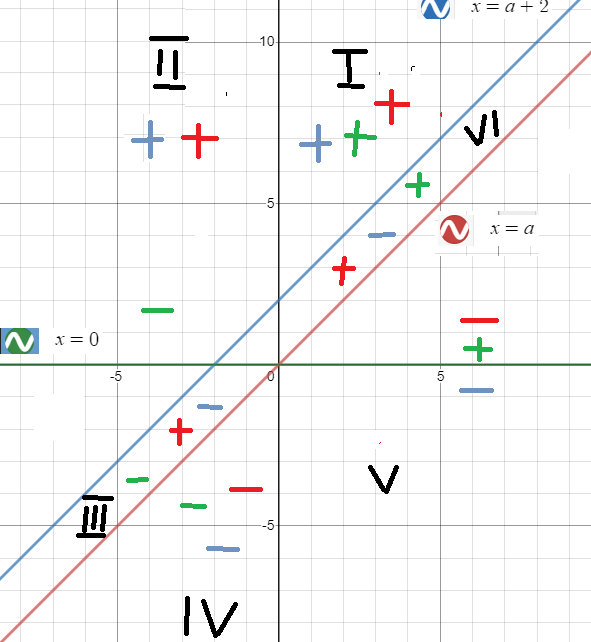
Прямые x=a+2 и x=a разбивают координатную плоскость хОа:
на три области: ( cм. рис.1)

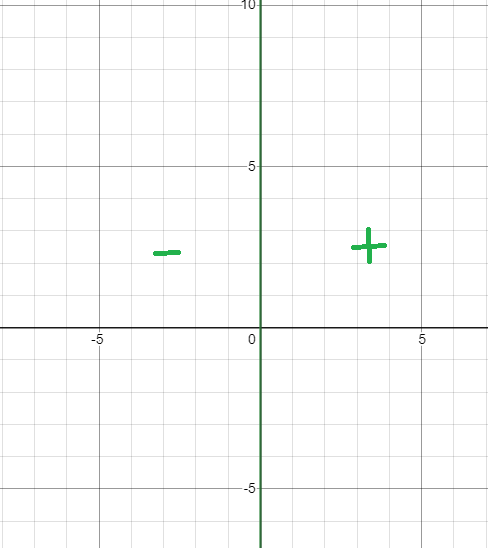
Прямая x=0 разбивает координатную плоскость на две части (рис.2)

Раскрываем знаки модулей в каждой области:
Первый случай:
[b]I:[/b]
{x ≥ 0;
{(x-a-2)*(x-a) ≥ 0

[red]a>0[/red]

Функция принимает вид:f(x)=x–2x+x^2–2(a+1)x+a^2+2a

f(x)=x^2-(2a+3)x+a^2+2a

Наим значение в вершине при x_(о)=(2a+3)/2

y_(o)=(2a+3)^2/4-(2a+3)^2/2+a^2+2a=(-4a-9)/4

(-4a-9)/4 > 4 ⇒ -4a-9 >16 ⇒ -4a > 25 и учитывая , что [red]a >0[/red]⇒ [b]a < -25/4[/b], что противоречит [red]a>0[/red]

Первый случай [i]не имеет решений.
[/i]

и так еще 5 раз :

Второй случай:
[b]II:[/b]
{x < 0;
{(x-a-2)*(x-a) ≥ 0
[green]a ≤
0[/green] в области [b]II:[/b]

Функция принимает вид:f(x)=x+2x+x^2–2(a+1)x+a^2+2a

f(x)=x^2-(2a-1)x+a^2+2a

Наим значение в вершине при x_(о)=(2a-1)/2
y_(o)=(2a-1)^2/4-(2a-1)^2/2+a^2+2a=(4a-1)/4 ⇒

(4a-1)/4 > 4 ⇒ 4a-1 > 16 ⇒ 4a > 17 и учитывая , что [green]a ≤ 0[/green]⇒ [b]a < 17/4[/b] ⇒ a ≤ 0

...