Задача 52727 Найдите все значения параметра, при...

tupiza

2020-06-26 18:20:52

Найдите все значения параметра, при которых уравнение

sqrt(x^(4)+x^(2)-5a^(2))=sqrt(x^(4)-4ax)

имеет ровно одно решение.

sova

2020-06-26 20:55:47

{x^4+x^2-5a^2 ≥ 0
{x^4-4ax ≥ 0
{x^4+x^2-5a^2=x^4-4ax ⇒ x^2+4ax-5a^2=0 ⇒ D=16a^2+20a^2=36a^2

x_(1)=[b]-5a[/b]; x_(2)=[b]a[/b]

Чтобы уравнение имело ровно одно решение
достаточно, чтобы один корень удовлетворял первым двум неравенствам, а второй не удовлетворял хотя бы одному из них

x=-5a
{(-5а)^4+(-5а)^2-5a^2 ≥ 0 ⇒ 625a^4+20a^2 ≥ 0 при любых а -
{(-5а)^4-4а*(-5а) ≥ 0 ⇒ 625a^4+20a^2 ≥ 0 при любых а -

x=-5a - корень уравнения


x=a
{(а)^4+(а)^2-5a^2 ≥ 0 ⇒ a^4-4a^2 ≥ 0
{(а)^4-4а*(а) ≥ 0 ⇒ a^4-4a^2 ≥ 0

a^2*(a-2)(a+2) ≥ 0 ⇒ (a-2)(a+2) ≥ 0 ⇒ a ∈ (- ∞;-2]U[2;+ ∞ )U{0} ⇒

a ∈ (-2;2)- наоборот, [red]x=a не является корнем уравнения[/red]

Осталось уточнить, что получаем при x=0

√x4+x2=√x4 ⇒ x=0 - корень уравнения, [i]единственный
[/i]

a=0 включаем в ответ

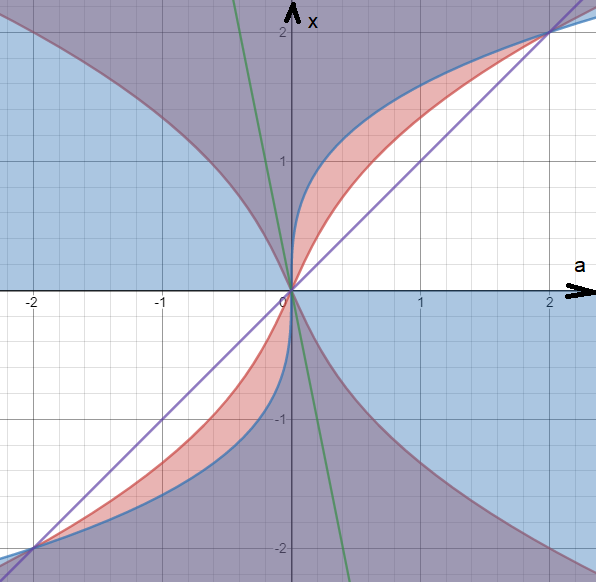
Геометрическая иллюстрация ( просто так для наглядности):

Построим множество точек плоскости xOа, удовлетворяющих неравенствам:
{x^4+x^2-5a^2 ≥ 0
{x^4-4ax ≥ 0

Системе удовл множество точек сиреневого цвета.
cм. рис.

Прямая x=-5a принадлежит полностью сиреневой области.

Прямая x=a принадлежит [b]НЕ полностью[/b] сиреневой области.

По рисунку видно, что x=a не принадлежит ОДЗ

при a ∈ [b](-2;2)[/b]