Задача 52544 ...
Условие
log₂((7^(-x^2)−6)(7^(-x^2+9)−1)) + log2 (7^(-x^2)-6)/(7^(-x^2+9)-1) > log2(7^(3-x^2)-5)^2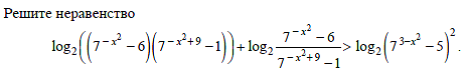
Решение
t>0
log_(2)(t-6)(7^9t-1)+log_(2)(t-6)/(7^(9)t-1)>log_(2)(7^(3)t-5)^2
Cумму логарифмов заменим логарифмом произведения:
log_(2)(t-6)^2>log_(2)(7^(3)t-5)^2 и с учетом ОДЗ получаем систему:
{log_(2)(t-6)^2>log_(2)(7^(3)t-5)^2
{(t-6)/(7^9t-1) >0 ⇒[b] t< 1/7^9[/b] или [b] t >6[/b]
{(t-6)*(7^9t-1) >0
{(7^(3)t-5)^2>0 ⇒ 7^(3)t-5 ≠ 1 ⇒[red] 7^3t ≠ 6[/red]
Решаем первое неравенство:
log_(2)(t-6)^2-log_(2)(7^(3)t-5)^2>0
Раскладываем на множители по формуле:a^2-b^2
[b]([/b]log_(2)(t-6)-log_(2)(7^3t-5)[b])[/b]*[b]([/b]log_(2)(t-6)+log_(2)(7^3t-5)[b])[/b]>0
log_(2)(t-6)/(7^3t-5) * log_(2)(t-6)*log_(2)(t-6)*(7^3t-5) >0
С учетом выделенных условий ОДЗ получаем ответ