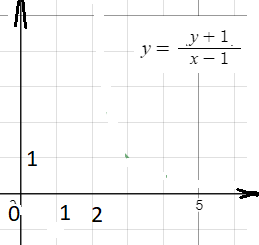Задача 52506 ...

vk302327408

17 июня 2020 г. в 12:57

– Найдите св–ва соответствий и отношений
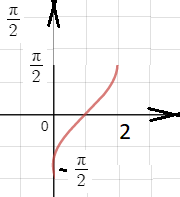
a) G={(x,y)∈R²|y=arcsin(x–1)}, δF={(x,y)∈N²|y= y+2/x–1}

sova

17 июня 2020 г. в 13:04

★

1.
–1 ≤ x–1 ≤ 1 ⇒ 0 ≤ x ≤ 2 ⇒ [0;2] → [–π/2;π/2]

Отношение монотонно, взаимно обратно.

2.
x ≠ 1

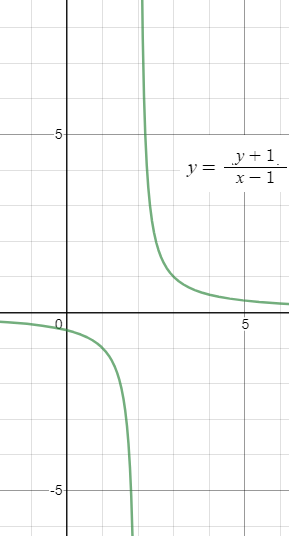
y·(x–1)=(y+1) ⇒ yx–y=y+1 ⇒ yx–2y=1 ⇒ y·(x–2)=1 ⇒ y=[m]\frac{1}{x-2}[/m]

x ≠ 2

График – точки с натуральными абсциссами, расположены на гиперболе y=[m]\frac{1}{x-2}[/m]( рис. 3)
кроме точек с абсциссами 1 и 2

Таких точек только одна (3;1)( рис. 2)