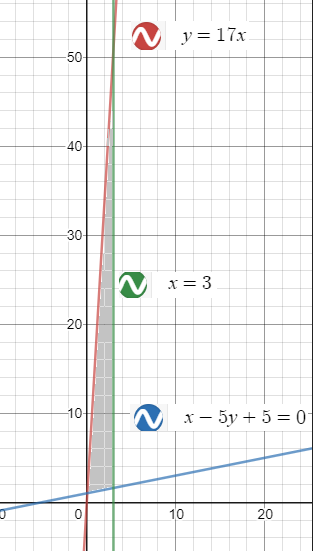
Задача 52421 Вычисли площадь фигуры, ограниченной...

vk185629374

14 июня 2020 г. в 12:50

Вычисли площадь фигуры, ограниченной линиями: y=17x,x−5y+5=0,x=3.

sova

14 июня 2020 г. в 18:42

Находим абсциссу точки пересечения
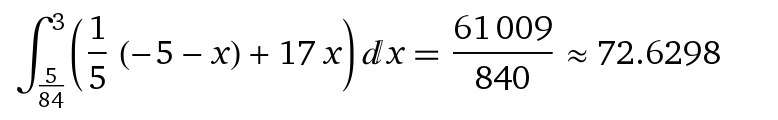
y=17x и x–5y+5=0

17х=(х+5)/5

85х=х+5

84х=5

х=5/84

S= ∫ ³_5/84(17x–(x+5)/5)dx= ∫ ³_5/84(84x–5)/5dx=

=((84/5)·(x²/2)–x)|³_5/84=(84/5)(9/2)–3–(42/5)·(5/84)²+(5/84)=

=(378/5)–3–(5/168)+(5/84)=61009/840 ≈ 72,6