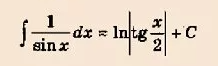Задача 52304 Вариант 5 1. Найти общее решение...

vk184048285

9 июня 2020 г. в 14:50

Вариант 5
1. Найти общее решение линейного ДУ–1:
1.1. xy' + y = 3

1.2. y – y/sin x = tg x/2

2. Решите задачу Коши:
y' = 2(x + y), если y(0) = 0

sova

9 июня 2020 г. в 20:31

1.

xy`=3–y – уравнение с разделяющимися переменными.

y`=dy/dx

dy/(3–y)=dx/x

∫ dy/(3–y)= ∫ dx/x

–ln|3–y|=ln|x|+lnC


1/(3–y)=Cx

2.

Линейное первого порядка. Решение в виде произведения двух функций

y=u·v

y`=u`·v+u·v`

u`·v+u·v`– (u·v)/sinx=tg(x/2)

Группируем:

u`·v+(u·v`– (u·v/sinx))=tg(x/2)

u`·v+u·(v`– (v/sinx))=tg(x/2)

Полагаем
v`– (v/sinx)=0

Это уравнение с разделяющими переменными

dv/v=dx/sinx

∫ dv/v =∫dx/sinx ( табличный интеграл, см формулу в приложении)

ln|v|=ln|tg(x/2)| ⇒ v=tg(x/2)

Тогда

u`tg(x/2)+u·0=tg(x/2)

Это уравнение с разделяющими переменными

u= x+C

y=u·v=(x+C)·tg(x/2)

О т в е т. y=x·tg(x/2) + C·tg(x/2)

3.
y`–2y=2x

Линейное первого порядка. Решение в виде произведения двух функций

y=u·v

y`=u`·v+u·v`


u`·v+u·v`–2u·v=2x

v`–2v=0 ⇒ dv/v=2dx ⇒ lnv=2x ⇒ ⇒ v=e^2x

u`·e^2x=2x

u`=2x/e^2x

u= ∫ e^–2x·(2x)dx= считаем по частям

...