Задача 52186 Помогите пожалуйста. Основанием...

vk247742080

2020-06-06 14:40:37

Помогите пожалуйста.
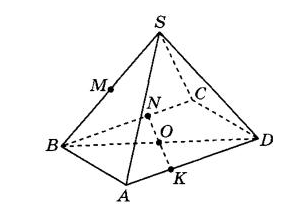
Основанием пирамиды SABCD является прямоугольник ABCD со сторонами АВ=15 и BC=25. Все боковые ребра пирамиды равны 5. На ребрах AD и ВС отмечены соответственно точки К и N так, что AK =CN =8. Через точки К и N проведена плоскость альфа, перпендикулярная ребру SB. Докажите, что плоскость альфа проходит через точку М - середину ребра SB. Найти расстояние между прямыми DS и КМ.

andriy

2020-06-06 14:57:32

★

Пусть точка О — пересечение BD и NK. Отрезки BN и KD равны и параллельны, поэтому точка О — середина BD. Рассмотрим треугольник BSD:
BD^(2)=BA^(2)+AD^(2)=15^(2)+25^(2)=850
BS^(2)+SD^(2)=2*5^(2)=50
Значит, треугольник BSD прямоугольный с прямым углом BSD.

Плоскость α перпендикулярна ребру BS, поэтому она параллельна прямой SD. Следовательно, плоскость α пересекает плоскость BSD по прямой, параллельной прямой SD, то есть по прямой ОМ, содержащей среднюю линию треугольника BSD.
Искомое расстояние равно расстоянию от прямой SD до параллельной ей плоскости α, содержащей прямую КМ. Следовательно, это расстояние равно длине перпендикуляра SM, проведённого от прямой SD к плоскости α.
SM=0.5*SB = 5/2 = 2.5