Задача 52119 Найти общее решение дифференциального...
Условие
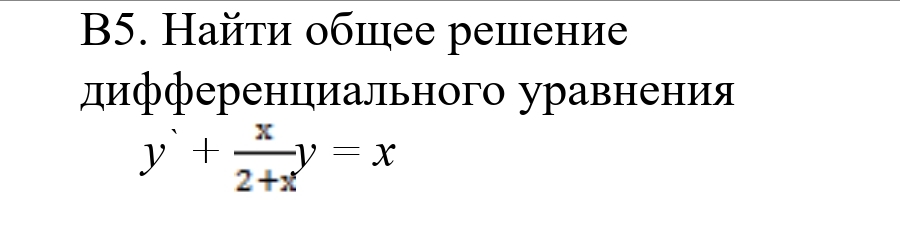
Все решения
Решают методом Бернулли или методом вариации произвольных постоянных
Метод Бернулли.
Решение ищем в виде
y=u*v
y`=u`*v+u*v`
Подставляем в уравнение
u`*v+u*v`+[m]\frac{x}{2+x}[/m]u*v=x
u`*v+u*(v`+[m]\frac{x}{2+x}[/m]*v)=x
Выбираем функцию v так, чтобы
1)
v`+[m]\frac{x}{2+x}[/m]*v=0
тогда
2)u`*v+u*0=x
Решаем два уравнения с разделяющимися переменными
1)[m]\frac{dv}{dx}=-\frac{x}{2+x}[/m]*v=0 ⇒ [m]\frac{dv}{v}=-\frac{xdx}{2+x}[/m]
[m] ∫ \frac{dv}{v}=- ∫ \frac{xdx}{2+x}[/m]
Cправа неправильная дробь, выделяем целую часть:
[m] ∫ \frac{dv}{v}=- ∫ \frac{x+2-2dx}{2+x}[/m]
[m] ∫ \frac{dv}{v}=∫ \frac{2dx}{2+x}- ∫ dx[/m]
⇒ ln|v|=2ln|x+2|-x ⇒ применяем свойства логарифмов
[m]v=\frac{(x+2)^2}{e^{x}}[/m]
Подставляем v во второе уравнение и находим u
u`*[m]\frac{(x+2)^2}{e^{x}}[/m]=x
Уравнение с разделяющимися переменными:
[m]du=\frac{xe^{x}}{(x+2)^2}dx[/m]
[m] ∫ du= ∫ \frac{xe^{x}}{(x+2)^2}dx[/m]
Справа интегрируем по частям ?
Задача непростая . Условие верное?
Как звучит вопрос? Может быть применение рядов к решению диф уравнений?