Задача 52118 (4 / ((1/3)^(x-1) - 9) - (1 / ((1/3)^x)...
Условие
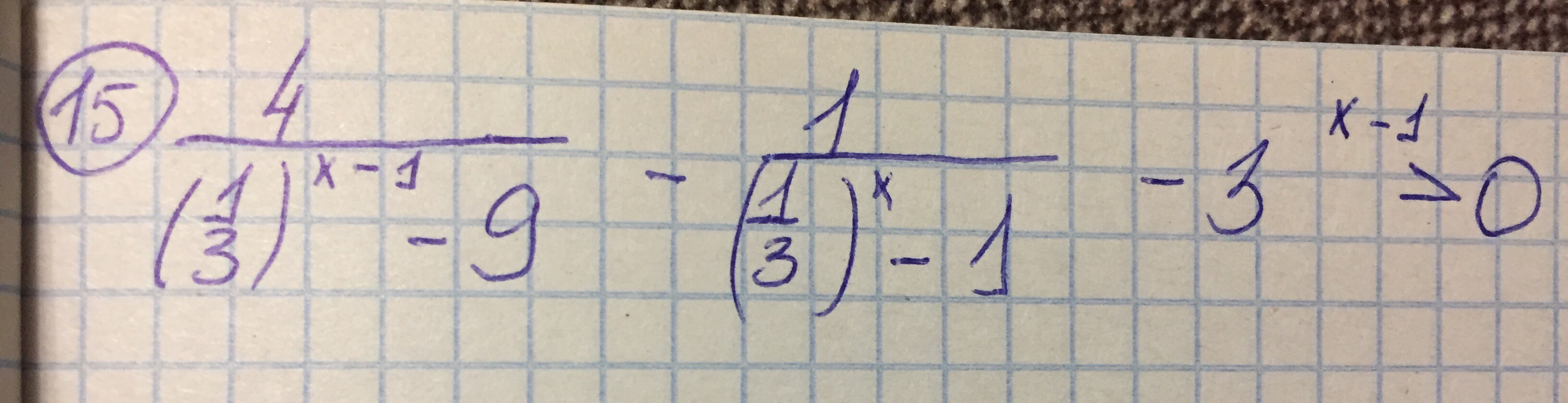
Все решения
[m](\frac{1}{3})^{x}=t[/m]
Показательная функция строго положительна, поэтому t > 0
[m](\frac{1}{3})^{x-1}=(\frac{1}{3})^{x}\cdot (\frac{1}{3})^{-1} =3(\frac{1}{3})^{x}=3t[/m]
[m]3^{x-1}=(\frac{1}{3})^{1-x}=\frac{1}{3}\cdot (\frac{1}{3})^{-x}=\frac{1}{3t}[/m]
Неравенство принимает вид:
[m]\frac{4}{3t-9}-\frac{1}{t-1}-\frac{1}{3t} >0[/m]
Приводим к общему знаменателю:
[m]\frac{4t(t-1)-3t(t-3)-(t-1)(t-3)}{3t(t-3)(t-1)} >0[/m]
Упрощаем числитель:
[m]\frac{9t-3}{3t(t-3)(t-1)} >0[/m]
Решаем неравенство методом интервалов:
Нули числителя:
9t-3=0 ⇒ t=[m]\frac{1}{3}[/m]
Нули знаменателя:
3t(t-3)(t-1)=0 ⇒ t=0; t=1; t=3
Знаки функции:
_+__ (0) __-_ ([m]\frac{1}{3}[/m] ) __+__ (1) __-___ (3) __+__
t < 0 или [m]\frac{1}{3}[/m] < t < 1 или t > 3
C учетом t >0
[m]\frac{1}{3}[/m] < t < 1 или t > 3
Обратный переход
[m]\frac{1}{3}<(\frac{1}{3})^{x} < 1[/m] или [m](\frac{1}{3})^{x}>3[/m]
Показательная функция с основанием [m]\frac{1}{3}[/m] убывающая, поэтому
0 < x < 1 или x < -1
О т в е т. (- ∞ ;-1) U (0;1)