Задача 52088 Площадь основания прямой призмы...
Условие
математика 10-11 класс
1351
Решение
★
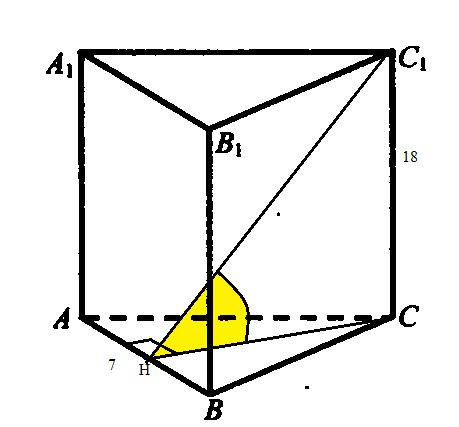
Тангенс угла между плоскостью основания призмы и плоскостью ABC1 будем искать из ΔС₁НС , где СС₁=18 .
ΔС₁НС , S=1/2*АВ*СН ,
15=1/2*7*СН,
СН=30/7.
tg∠С₁НС=СС1/СН ,tg∠С₁НС=4,2