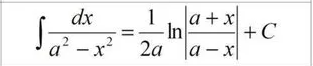Задача 51900 помогите пожалуста до 11:30 все что...

vk230371874

2020-05-29 09:49:52

помогите пожалуста до 11:30 все что можно
вот приблизительный перевод
1. Свойства неопределенного интеграла.
2. Системы дифференциальных уравнений. Методы решения.
3. Найдите указанные корни.
4. Используйте дифференциал, чтобы оценить данное выражение.
5. Найдите определенный интеграл.
6. Решите дифференциальное уравнение.

sova

2020-05-29 11:25:29

★

5.
x-1=t
x=t+1

x^2=(t+1)^2=t^2+2t+1

dx=dt

Пределы: если x=5, то t=4
если x=2, то t=1

[m]\int^{5}_{2}\frac{x^2dx}{(x-1)\sqrt{x-1}}=\int^{4}_{1}\frac{t^2+2t+1}{t\sqrt{t}}dt=[/m]

[m]= \int^{4}_{1}(\sqrt{t}+\frac{2}{\sqrt{t}}+\frac{1}{t\sqrt{t}})dt=[/m]

[m]= \int^{4}_{1}(t^{\frac{1}{2}}+2\cdot t^{-\frac{1}{2}}+ t^{-\frac{3}{2}})dt=[/m]

[m]=(\frac{2}{3}\cdot t^{\frac{3}{2}}+4t^{\frac{1}{2}}-2t^{-\frac{1}{2}})|^{4}_{1}=7+\frac{8}{3}=9\frac{2}{3}[/m]

6.
x^2(1-y^2)dx=-y^2(1-x^2)dy - уравнение с разделяющимися переменными

x^2dx/(1-x^2)=-y^2dy/(1-x^2)

Прибавим 1- вычтем 1 в числителях

[m]\frac{x^2-1+1}{1-x^2}dx=\frac{1-1-y^2}{1-y^2}dy[/m]

Интегрируем


[m] ∫ (-1+\frac{1}{1-x^2})dx= ∫ (\frac{1}{1-y^2}+1)dy[/m]


[m]-x+\frac{1}{2}ln|\frac{1+x}{1-x}|=\frac{1}{2}ln|\frac{1+y}{1-y}|+y+lnC[/m]