Задача 51794 ...
Условие
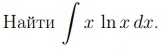
математика ВУЗ
630
Решение
★
Решение:
Интегрируем по частям по формуле : ∫ f(x)dg(x)=f(x)g(x)- ∫ g(x)df(x)
Пусть f(x)=lnx и xdx=dg(x), тогда df(x)=dx/x и g(x)=x^2/2 подставим
в формулу интегрирования по частям находим
∫ x lnx dx= ∫ lnxd(x^2/2)=x^2/2 lnx- ∫ x^2/2 d lnx=x^2/2 lnx- ∫ x/2 dx=x^2/2 lnx-x^2/4+C=x^2/2(ln x-1/2)+C

