Задача 51607 ...

hades202

26 мая 2020 г. в 11:16

Основанием прямой призмы ABCKLN является равнобедренный треугольник.
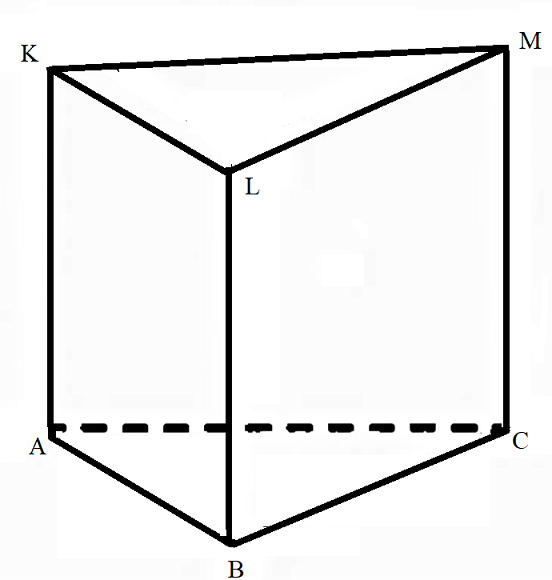
Площадь грани AKLB равна 263–√ см2, угол ACB=120°, AC=CB= 16 см. Вычисли площадь основания и высоту призмы.

trijstura prizma 1.JPG

Ответ:
площадь основания призмы равна
−−−−−−−√ см2

(если в ответе корней нет, то под корнем пиши 1).

sova

23 июля 2020 г. в 13:40

Основанием призмы ABCKLN является равнобедренный треугольник.
угол ACB=120°, AC=CB= 16 см.

По теореме косинусов:
АВ²=AC²+BC²–2AC·BC·cos120 ° =16²+16²–2·16·16·(–1/2)=16²·3

AB=4√3

S _{Δ ABC}=(1/2)AC·BC·sin120 ° =(1/2)·16·16·(√3)/2=64√3 cм²

Призма прямая, значит боковые ребра АК, BL и СM перпендикулярны плоскости АВС.
Грань АКLB – прямоугольник.

По условию "Площадь грани AKLB равна 263√3 см²" и АВ=ВС=16 см

S_AKLB=AB·AK ⇒ АК= [m]\frac{S_{AKBL}}{AB}=\frac{263\sqrt{3}}{4\sqrt{3}}=\frac{263}{4}[/m]

Н_призмы=АК=[m]\frac{263}{4}[/m]