Задача 51602 Помогите, доказать. Пожалуйста ...
Условие
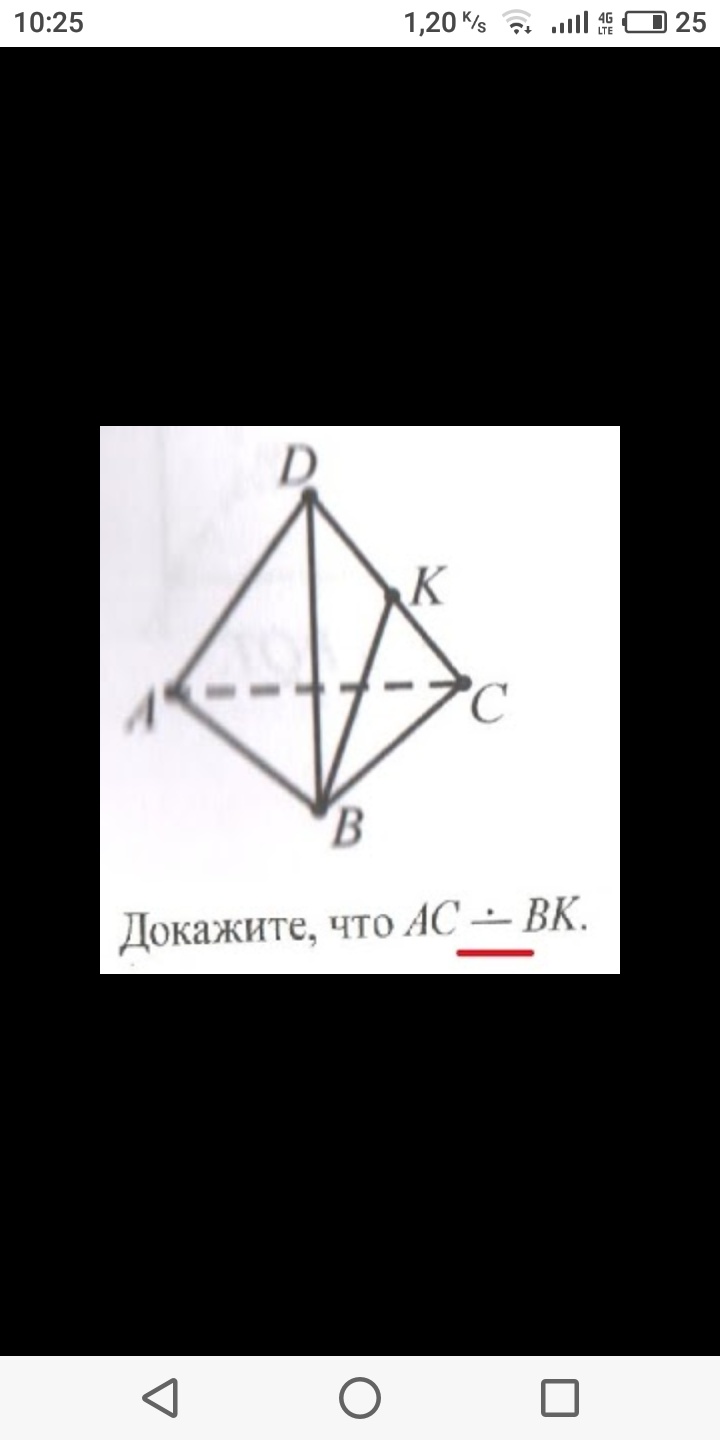
математика 10-11 класс
761
Все решения
!) Признак скрещивающихся прямых:
Если одна из двух прямых лежит в некоторой плоскости
а другая прямая пересекает эту плоскость в точке нележащей на первой прямой то эти прямые скрещивающиеся.
2) Прямая АС лежит в плоскости (АВС)
3)Точка В не принадлежит прямой АС
4) Прямая ВК пересекает плоскость (АВС) в точке В
5) По признаку скрещивающихся прямых прямые АС и ВК-скрещивающиеся.
