Задача 51569 Площадь полной поверхности конуса равна...

vk288952222

25 мая 2020 г. в 20:35

Площадь полной поверхности конуса равна 32,5. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 4 : 1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

sova

25 мая 2020 г. в 20:40

★

S_{полн. конуса}=S_бок+S_осн=π·R·L+π·R²

S_{полн. конуса}=32,5

π·R·L+π·R²=32,5


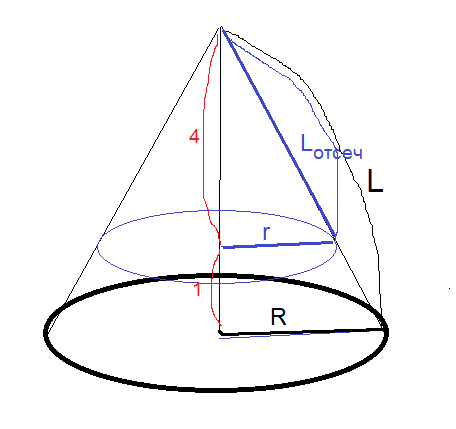
r_сеч:R=4:5 ⇒ r_сеч=(4/5)·R

L_{отсеч. конуса}:L=4:5 ⇒ L_{отсеч. конуса}=(4/5)·L


S_{полн. отсеч. конуса}=S_сеч+S_{бок. отсеч конуса}=

=π·r²+π·r·L_{отсеч. конуса}=

=π·((4/5)·R)²+π·((4/5)R)·(4/5)·L=

=(16/25)π·R²+(16/25)πRL

так как
π·R·L+π·R²=32,5

=(16/25)(π·R²+πRL)=(16/25)·32,5=0,64·32,5=20,8

vk397114329

25 мая 2020 г. в 22:43

Отсеченная часть конуса подобна данному конусу. k=4/5
Отношение площадей подобных фигур равно квадрату коэффициента подобия
Получаем: Sотсеч/Sдан=(4/5)² По условию Sдан=32,5 Отсюда Sотс=32,5·16/25=20,8
Ответ:20,8