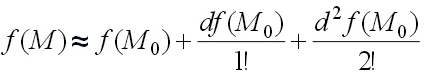Задача 51315 Помогите решить пожалуйста. 11.7.6....

vk169585692

2020-05-22 19:36:12

Помогите решить пожалуйста.
11.7.6.

sova

2020-05-22 20:12:07

★

Все [i]приближенные[/i] вычисления основаны на[i] приближенном[/i] равенстве ( cм. приложение)

Слева -значение функции в "нехорошей" точке M(x_(o)+ Δx;y_(o)+ Δy) , справа-значение функции в "хорошей" точке M_(o)(x_(o);y_(o)) и частные производные в "хорошей" точке M_(o)(x_(o);y_(o))


180 ° =π рад ⇒ 1 ° =(π/180) радиан

x_(o)=45 ° =(π/4)

x_(o)+ Δx=47 ° ⇒ Δх=2 ° =2*(π/180)=(π/90) радиан

y_(o)=30 ° = (π/6)

x_(o)+ Δx=28 ° ⇒ Δy=-2 ° =-2*(π/180)=(-π/90) радиан

df(x_(o);y_(o))=f`_(x)(x_(o);y_(o)) Δx+f`_(y)(x_(o);y_(o)) Δy

f`_(x)(x;y)=siny*(tgx)`_(x)=siny/cos^2x

f`_(y)(x;y)=tgx*(siny)`_(y)=tgx*cosy

f`_(x)(x_(o);y_(o))= f`_(x)(π/4;π/6)= sin(π/6)/cos^2(π/4)=1

f`_(y)(x_(o);y_(o))= f`_(y)(π/4;π/6)= tg(π/4)*cos(π/6)=1*sqrt(3)/2


df(x_(o);y_(o))=df(π/4;π/6)=1*(π/90)+(sqrt(3)/2)*(-π/90) ≈ считаем и подставляем в формулу


d^2(x_(o);y_(o))=f``_(xx)(x_(o);y_(o)) (Δx)^2+2f``_(xy)(x_(o);y_(o)) Δx* Δy+f``_(xx)(x_(o);y_(o)) (Δx)^2


f ``_(xx)(x;y)=(siny/cos^2x)`_(x)=2siny*(sinx)/cos^3x


f ``_(xy)(x;y)=(siny/cos^2x)`_(y)=cosy/cos^2x


f ``_(yy)(x;y)=(tgx*cosy)`_(y)=-tgx*siny




f ``_(xx)(x_(o);y_(o))=f ``_(xx)(π/4;π/6)=2


f ``_(xy)(x_(o);y_(o))=f ``_(xy)(π/4;π/6)=sqrt(3)


f ``_(yy)(x_(o);y_(o))=f ``_(yy)(π/4;π/6)=-1/2


d^2(x_(o);y_(o))=d^2(π/4;π/6)=2*(π/90)^2+2sqrt(3)*(π/90)*(-π/90)-(1/2)*(-π/90)^2 ≈ считаем и подставляем в формулу