Задача 50959 ...
Условие
{ log^2_(|x|) (x^2) + log_2 (x^2) ≤ 8.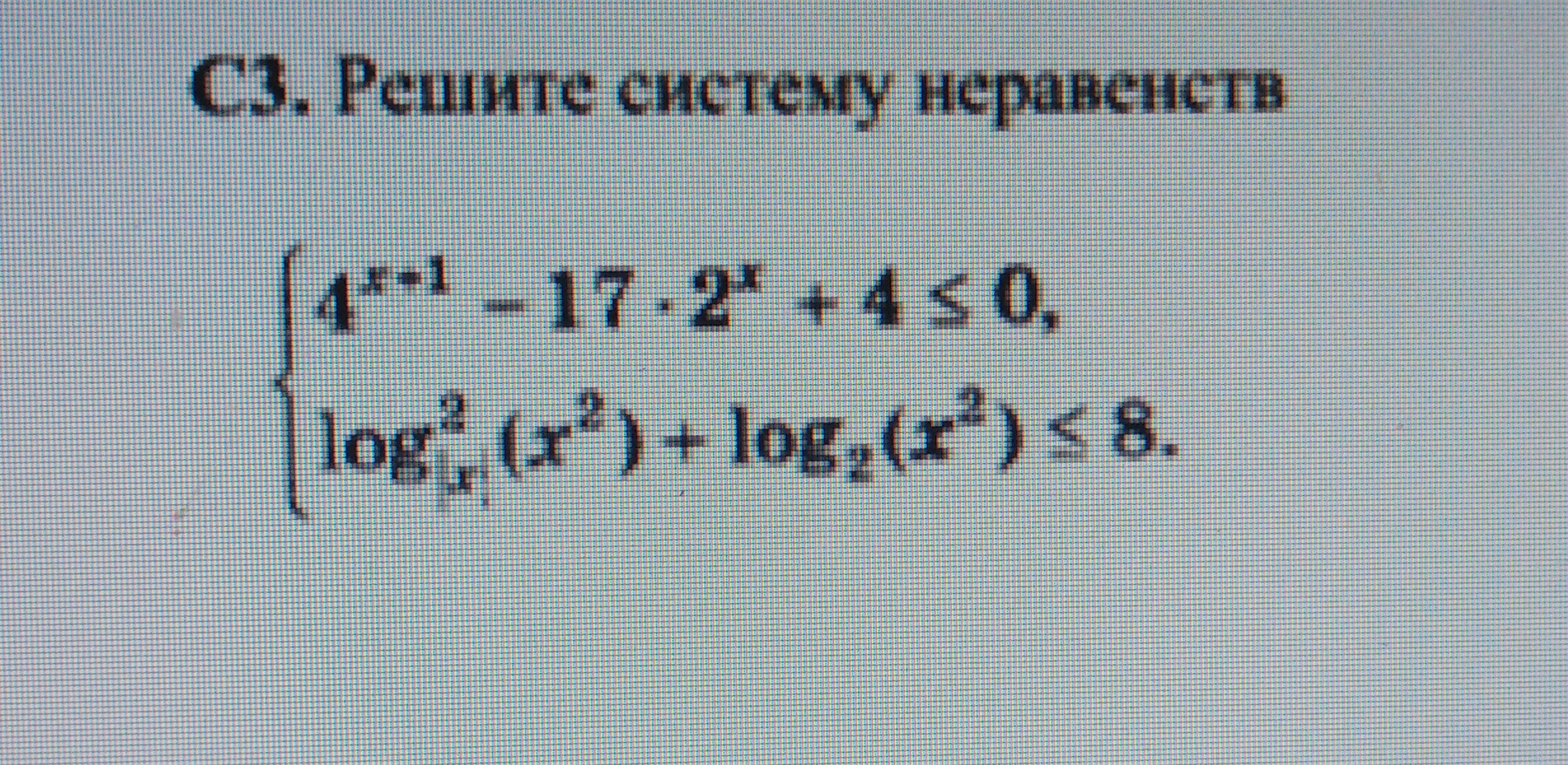
предмет не задан
654
Все решения
{x^2>0 ⇒ [red]x ≠ 0[/red]
{|x| ≠ 1 ⇒ [red]x ≠ ± 1[/red]
log_(|x|)x^2=log_(|x|)(|x|)^2=2log_(|x|)(|x|)=2
log^2_(|x|)x^2=2^2=4
{4*(2^(x))^2-17*2^(x)+4 ≤ 0 ⇒ D=225; (1/4) ≤ 2^(x) ≤ 4
{4+log_(2)x^2 ≤ 8 ⇒ (log_(2)x-2)*(log_(2)x+2) ≤ 0 ⇒ -2 ≤ log_(2)x ≤ 2
{2^(-2) ≤ 2^(x) ≤ 2^2 ⇒ (-2) ≤ x ≤ 2
{log_(2)(1/4) ≤ log_(2)x ≤ log_(2)4 ⇒ (1/4) ≤ x ≤ 4
(1/4) ≤ х ≤ 2
C учетом ОДЗ
О т в е т. [1/4;1) U (1; 2]