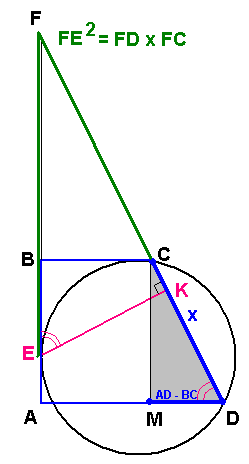
Задача 50949 В трапеции ABCD боковая сторона AB...

help

2020-05-20 11:02:56

В трапеции ABCD боковая сторона AB перпендикулярна основанию ВС. Окружность проходит через точки С и D и касается прямой AB в точке Е. Найдите расстояние от точки Е до прямой CD, если AD = 6, ВС = 5.

morcovcaiq

2020-05-20 11:13:32

★

AD=6, BC=5
MD = 6 – 5 = 1

∆CDM ∞ ∆FCB
MD : BC = CD : FC
1 : 5 = x : FC
FC = 5x

FE2 = FD ∙ FC
FE2 = (FC + CD) ∙ FC
FE2 = 6x ∙ x
FE = √6 x

∆FKE (∠K = 90o)
EK = FE ∙ cos E = FE ∙ cos D = = FE ∙ MD/CD = √6 x ∙ 1/x = √6

Ответ: √6