Задача 50889 и вот ещё последние пж)))...
Условие
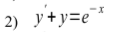
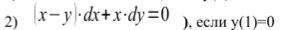
предмет не задан
566
Решение
★
y=u*v
y`=u`*v+u*v`
u`*v+u*v`+u*v=e^(-x)
v`+v=0 ⇒ dv/v=-dx ⇒ lnv=-x ⇒ [b] v=e^(-x)[/b]
u`*[b]v[/b]=e^(-x)
u`*[b]e^(-x)[/b]=e^(-x)
u`=1
u=x+c
y=u*v
y=[b](x+C)*e^(-x)[/b]
2)
(x-y)=-x*y`
y`=(x-y)/y
y`= φ (x/y)
Значит, замена:
[b]y/x=u[/b]
y=ux
y`=u`*x+u
x-ux=-x*(u`*x+u)
x-ux=-x*u`*x-xu
x=-x^2*u`
1=-x*u`
u`=-1/x
du=-dx/x
u=-ln|x|+lnC
u=ln(C/x)
y=u*x
y=x*ln(C/x)
[b]x=1; y=0[/b]
0=1*lnC
C=1
[b]y=x*ln(1/x)[/b]
