Задача 50881 ...
Условие
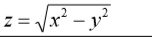
математика
646
Решение
★
∂z/ ∂y=z`_(y)=[m](x^2-y^2)^{\frac{1}{2}}=\frac{1}{2}\cdot (x^2-y^2)^{\frac{1}{2}-1}\cdot (x^2-y^2)`_{y}=\frac{y}{\sqrt{x^2-y^2}}[/m]