Задача 50861 ...
Условие
x/у . ∂²z/∂x² + у/x . ∂²z/∂y² – 2 ∂²z/∂x∂y + 2/у . ∂z/∂x = 0.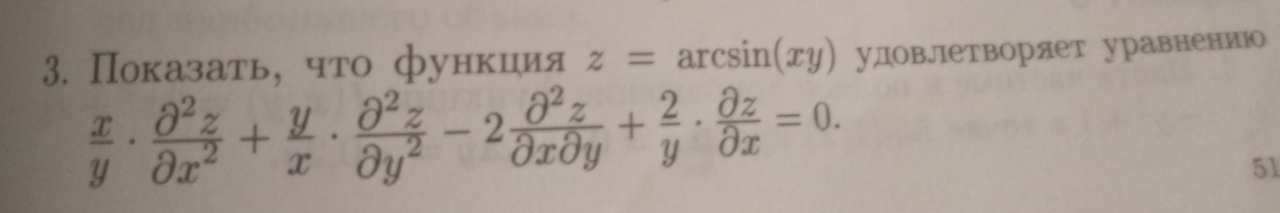
Решение
∂z/ ∂y=[m]\frac{1}{\sqrt{1-(xy)^2}}\cdot (xy)`_{y}=\frac{x}{\sqrt{1-(xy)^2}}[/m].
∂2z/ ∂x2=[m](\frac{y}{\sqrt{1-(xy)^2}})`_{x}=y\cdot ((1-(xy)^2)^{-\frac{1}{2}})`_{x}=[/m]
[m]=-\frac{1}{2}y(1-x^2y^2)^{-\frac{3}{2}}\cdot(1-x^2y^2)`_{x}=\frac{xy^3}{\sqrt{(1-x^2y^2)^3}}[/m];
∂2z/ ∂x ∂y=[m](\frac{y}{\sqrt{1-(xy)^2}})`_{y}=(y\cdot (1-(xy)^2)^{-\frac{1}{2}})`_{y}=[/m]
[m]= (1-(xy)^2)^{-\frac{1}{2}}+(-\frac{1}{2})y(1-x^2y^2)^{-\frac{3}{2}}\cdot(1-x^2y^2)`_{y}=[/m]
[m]=\frac{1}{\sqrt{1-x^2y^2}}+\frac{x^2y^2}{\sqrt{(1-x^2y^2)^3}}=\frac{1}{\sqrt{(1-x^2y^2)^3}}[/m];
∂2z/ ∂y2=[m](\frac{x}{\sqrt{1-(xy)^2}})`_{y}=x\cdot ((1-(xy)^2)^{-\frac{1}{2}})`_{y}=[/m]
[m]=-\frac{1}{2}x(1-x^2y^2)^{-\frac{3}{2}}\cdot(1-x^2y^2)`_{y}=\frac{x^3y}{\sqrt{(1-x^2y^2)^3}}[/m].
Подставляем в уравнение и получаем доказательство