Задача 50807 Помогите решить с графиком!!!!!!!...

vk280770680

19 мая 2020 г. в 14:00

Помогите решить с графиком!!!!!!!

sova

19 мая 2020 г. в 15:49

★

Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Составляем характеристическое уравнение:

k²–3k–4=0
D=9+16=25

k₁=–1; k₂=4 – корни действительные различные,

поэтому общее решение однородного уравнения с постоянными коэффициентами имеет вид:

y_{общее одн}=C₁e^–1·x+C₂e^4·x – общее решение однородного уравнения


Частное решение:

Так как y(0)=1,
то
1=C₁e^–1·0+C₂e^4·0 ⇒1=C₁+C₂

Так как y ` (0)=–2

находим y`

y`=(C<sub>1</sub>e<sup>–1·x</sup>+C<sub>2</sub>e<sup>4·x</sup>)`=C₁·(e^–x)`+C<sub>2</sub>·(e<sup>4x</sup>)`=

=C₁·e^–x·(–x)`+C<sub>2</sub>·e<sup>4x</sup>·(4x)`=

=C₁·e^–x·(–1)+C₂·e^4x·(4)=

=–C₁·e^–x+4·C₂·e^4x


–2=–C₁+4·C₂

Решаем систему:
{1=C₁+C₂
{–2=–C₁+4·C₂

Cкладываем:

–1=5С₂

С₂=–1/5=–0,2

С₁=1–С₂=1–(–0,2)=1,2

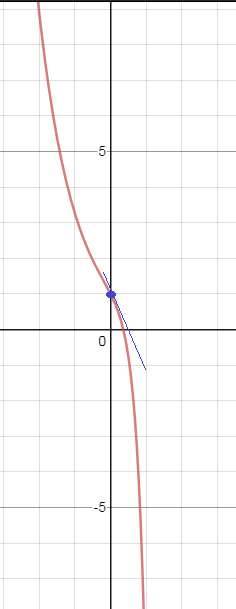
О т в е т. y=1,2e^–1·x–0,2·e^4·x – решение задачи Коши.

Это кривая, которая проходит через точку (0;1) и имеет в этой точке угловой коэффициент касательной, равный (–2)