Задача 50741 Помогите пожалуйста решить !!!! ...
Условие
Решение
p=0,005
q=1-p=1-0,005=0,995
Повторные испытания с двумя исходами. Теорема Пуассона.
np=5
npq=4,975
a)
λ =np=5
событие A - " не более трех знаков"
Значит 0; 1; 2;3
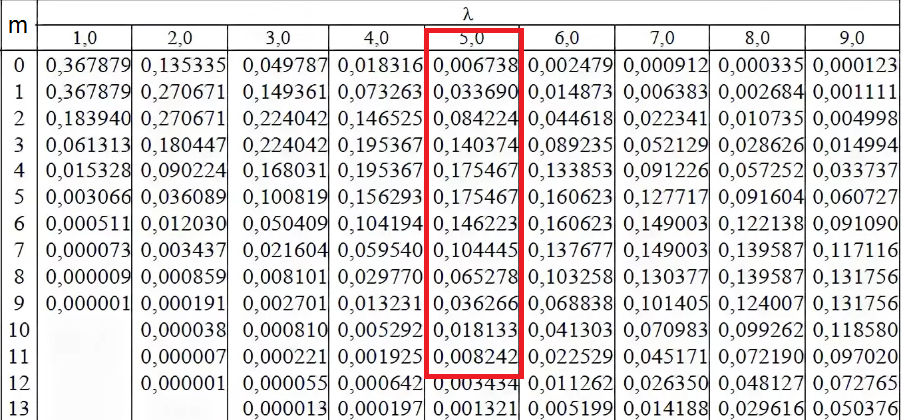
Применяем формулу Пуассона
m=0
P_(1000)(0)= (5)^(0)/0!)e^(-5) ≈ 0,006738
( значение в таблице )
m=1
P_(1000)(1)= ((5)^(1)/1!)e^(-5) ≈ 0,033690
m=2
P_(1000)(2)= ((5)^(2)/2!)e^(-5) ≈ 0,084224
m=3
P_(1000)(3)= ((5)^(3)/3!)e^(-5)=
p(A)=P_(1000)(0)+P_(1000)(1)+P_(1000)(2)+P_(1000)(3) ≈
≈ 0,006738+0,033690+0,084224+
О т в е т.
б) событие B - " будет искажено более 10-ти знаков"
Рассмотрим противоположное событие
vector{В} - "искажено не более 10-ти знаков"
Значит 0,1,2,3,4,5,6,7,8.9,10
Считаем как пункте а)
P(vector{В})=P_(1000)(0)+P_(1000)(1)+P_(1000)(2)+...P_(1000)(10)=...
p(B)=1-p(vector{B})= ...
в)
решено в б)
P(vector{В})=P_(1000)(0)+P_(1000)(1)+P_(1000)(2)+...P_(1000)(10)=...
