Задача 50333 Боковое ребро правильной треугольной...

tupiza

2020-05-15 23:57:24

Боковое ребро правильной треугольной пирамиды SABC равно 10, а косинус угла ASB при вершине боковой грани равен 1/16. Точка M — середина ребра SC.
а) Докажите, что BC перпендикулярно AS.
б) Найдите косинус угла между прямыми BM и SA.

Легче понимаю координатный способ, но любое решение подойдет

xacku13052020

2020-05-16 07:31:47

а)Пусть SO⊥(ABC) Тогда, точка О -центр правильного треугольника( лежит в точке пересечения медиан).
Т.к. прямая лежащая в плоскости ВС ⊥АО, то и наклонная SA⊥ВС по т. о трех перпендикулярах .
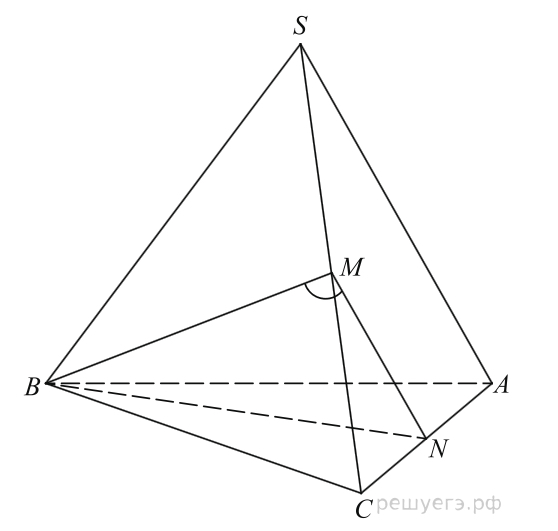
б)Пусть МN||SA , тогда ∠ВМN-искомый.
ΔSAC , МN- средняя линия ZS, МN=5
ΔВSМ , по т. косинусов ВМ²=SM²+SB²-2*SM*SB*cosBSM ,
cosBSM=cosASB,
ВМ²=5²+10²-2*5*10*(1/16) ,
ВМ=2,5√19.
ΔВSС , по т. косинусов ВС²=SС²+SB²-2*SС*SB*cosBSM ,
ВС=√(2*100-2*100*(1/16))= 2,5√30
1/2ВС=1,25√30
ΔВРС-прямоугольный, по т. Пифагора :
ВN=3,75√30
ΔВРN, по т. косинусов ВN²=ВМ²+NМ²-2*ВМ*NМ*cosBMN ,
(3,75√30)²= (2,5√19)²+5²-2*(2,5√19)*5*cosBMN ,
///////////////////////////////
cosBMN =1/(8√19 )= √19/152