Задача 50083 ...
Условие
Решение
{cosx ≠ 0 ( потому что он в знаменателе tgx и тогда tgx не сущ)
{65cos^2x+56cosx=0
{56tgx-33 ≠ 0
65cos^2x+56cosx=0
cosx*(65cosx+56)=0
cosx=0 или 65 cosx-56=0 ⇒
cosx=-56/65
x= ± arccos(-56/65)+2πn, n ∈ Z
Но tgx ≠ 33/56 ⇒
Если cosx=-56/65, то sin^2x=1-cos^2x
sin^2x=1- ([m]-\frac{56}{65}[/m])^2=[m]\frac{65^2-56^2}{65^2}[/m]
cosx < 0; tgx >0 ⇒ sinx <0
sinx=-[m]\frac {33}{65}[/m] ⇒ tgx =[m]\frac {33}{56}[/m]
т. е корни из третьей четверти не входят в ответ
Значит, в ответ входит
х= arccos(-56/65)+2πn, n ∈ Z
x=π-arccos(56/65)+2πn, n ∈ Z
б) π- arccos(56/65)-12π=-11π-arccos(56/65) - корень, принадлежащий указанному промежутку.
-25π/2 < -11π-arccos(56/65) < - 11π
---- ---- ---- ---- ---- ---- ---- ----
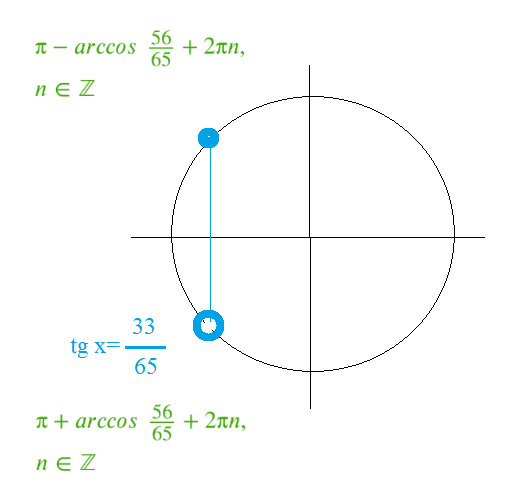
Все решения
