Задача 50050 ...

bababa

2020-05-13 13:51:07

Функция плотности распределения случайной величины ξ имеет следующий вид:
f(x) =
{ 0, если x ∉ [4; 6]
{ c, если 4 ≤ x < 5
{ cx, если 5 ≤ x ≤ 6.

Построить график f(x) и найти P(ξ < 5).

sova

2020-05-13 14:02:21

★

∫ ^(+ ∞ )_(- ∞ )f(x)dx=1

∫ ^(4)_(- ∞ )[b]0[/b]dx+ ∫^(5)_(4)cdx+ ∫ ^(6)_(5)cxdx+ ∫ ^(+ ∞ )_(6)[b]0[/b]dx=1

c*x|^(5)_(4)+c*(x^2/2)|^(6)_(5)=1

с*(5-4)+с(18-12,5)=1

6,5с=1

с=2/13

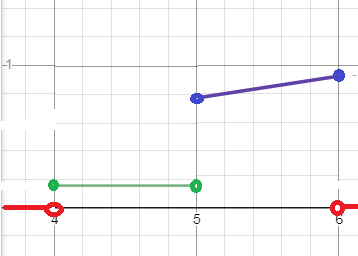
График такой:

на (- ∞; 4) y=0 красного цвета, справа "дырка"

на [4;5) y=2/13 зеленая,

на [5;6] y=(2/13)x сиреневая

на (6;+ ∞ ) y=0 красного цвета

P( ξ <5)= ∫ ^(5)_(- ∞ )f(x)dx= ∫ ^(5)_(4)(2/13)dx=(2/13)*(5-4)=2/13

'это площадь под графиком y=2/13
А там прямоугольник.

Функция распределения - первообразная от f(x)