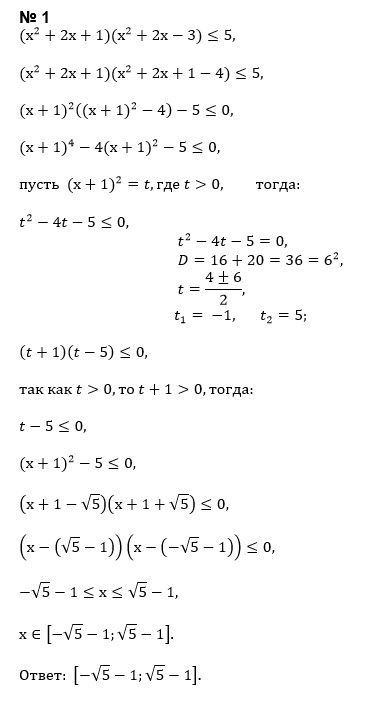Задача 50011 помогите пожалуйста. СРОЧНО ...

chappie06

2020-05-13 12:19:59

помогите пожалуйста. СРОЧНО

sova

2020-05-13 15:00:20

1.
[blue]Замена переменной[/blue]

x^2+2x-3=t

x^2+2x+1=t+4

t*(t+4) ≤ 5

t^2+4t-5 ≤ 0

D=16+20=36

t_(1)=-5; t_(2)=1

___ [-5] __[green]-[/green]___ [1] ____

-5 ≤ t ≤ 1

-5 ≤ x^2+2x-3 ≤ 1

{x^2+2x-3 ≤ 1
{x^2+2x-3 ≥ -5

{x^2+2x-4≤ 0 ⇒ D=20 ⇒ -1 - sqrt(5) ≤ x ≤ -1 + sqrt(5)
{x^2+2x+2 ≥ 0 ⇒ D=4-4*2<0 неравенство верно при любом х


О т в е т. [ -1 - sqrt(5) ;-1 + sqrt(5)]


2.

5^(x+1)=5^(x)*5
[blue]Замена переменной[/blue]

5^(x)=t

t >0

5^(-x)=1/t

5t +([b]3[/b]/t) ≤ 16

Умножаем на t ≥ 0

5t^2-16t+[b]3[/b] ≤ 0

D=(-16)^2-4*5*3=256-60=196

t_(1)=(16-14)/10=1/5; t_(2)=(16+14)/10=3

Решение неравенства:

(1/5) ≤ 5^(x) ≤ 3

5^(-1) ≤ 5^(x) ≤ log_(5)3

О т в е т. [1/5; log_(5)3]