Задача 49829 ...

apricot

12 мая 2020 г. в 09:44

• №1

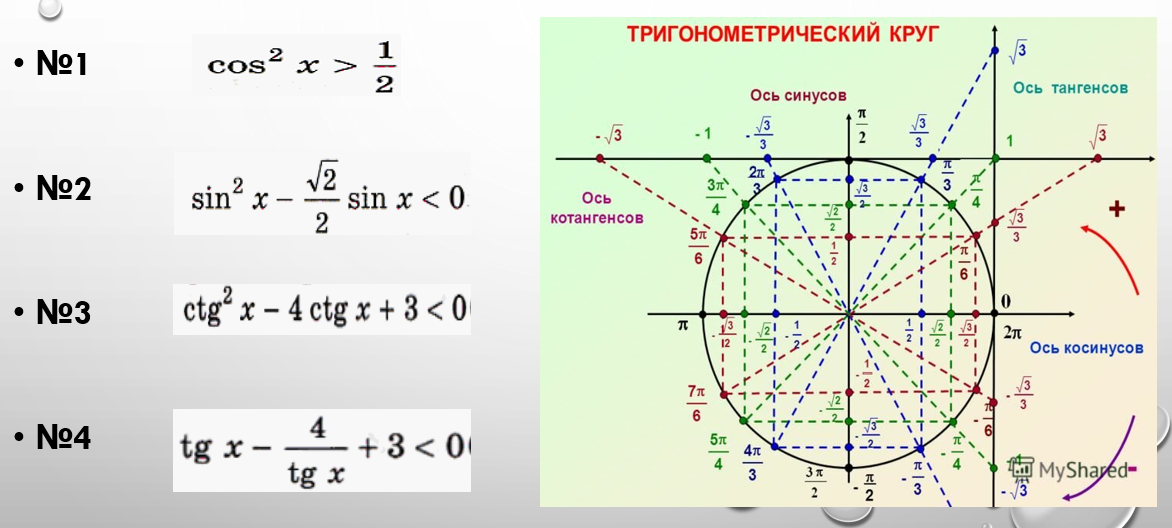
cos²x > 1/2

• №2

sin²x – √2/2 sin x < 0

• №3

ctg²x – 4 ctg x + 3 < 0

• №4

tg x – 4/tg x + 3 < 0

sova

12 мая 2020 г. в 17:43

★

1.
[m]\begin{matrix} cosx<- \frac{\sqrt{2}}{2}& ;cosx >\frac{\sqrt{2}}{2} & \end{matrix}[/m]

[m]\begin{matrix} \frac{3\pi}{4}+2\pi n <x<\frac{5\pi}{4}+2\pi n & ;-\frac{\pi}{4}+2\pi n <x<\frac{\pi}{4}+2\pi n, n \in Z & \end{matrix}[/m]

2.
[m]\begin{matrix}sinx\cdot (sinx- \frac{\sqrt{2}}{2}) <0& \end{matrix}[/m]

[m]\begin{matrix}sinx <0 &; sinx> \frac{\sqrt{2}}{2}& & \end{matrix}[/m]

[m]\begin{matrix}\pi +2 \pi n < x < 2 \pi +2\pi n, &; \frac{\pi}{4}+2\pi n <x< \frac{3 \pi}{4}+2\pi n, n \in Z& \end{matrix}[/m]

3.
ctgx=t
t²–4t+3 <0
D=16–4·3=16–12=4
t₁=1; t₂=3

1 < t < 3

1 < ctgx < 3

y=ctgx – убывающая функция, бОльшему значению функции соответствует мЕньшее значение аргумента

[m]\begin{matrix}arctg3 + \pi n < x < \frac{\pi}{4}+\pi n , n \in Z& \end{matrix}[/m]