Задача 49671 Вычислить несобственный интеграл или...
Условие
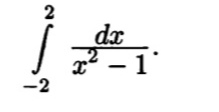
Все решения
Разбиваем интеграл на сумму четырех интегралов
∫ ^(-1)_(-2)[m]\frac{dx}{x^2-1}[/m]+ ∫ ^(0)_(-1)[m]\frac{dx}{x^2-1}[/m]+ ∫ ^(1)_(0)[m]\frac{dx}{x^2-1}[/m]+ ∫ ^(2)_(1)[m]\frac{dx}{x^2-1}[/m]
Все три -несобственные интегралы 2 рода
lim_( a → -1-0) ∫ ^(a)_(-2)[m]\frac{dx}{x^2-1}[/m]+lim_( b → -1+0)∫ ^(0)_(b)[m]\frac{dx}{x^2-1}[/m]+
+lim_( c → 1-0) ∫ ^(c)_(0)[m]\frac{dx}{x^2-1}[/m]+lim_( d → 1+0)∫ ^(2)_(d)[m]\frac{dx}{x^2-1}[/m]=
([i]табличный интеграл[/i] [m]\int \frac{dx}{x^2-1}=ln|\frac{x-1}{x+1}|[/m])
=lim_( a → -1-0)[m] ln|\frac{a-1}{a+1}|-ln|\frac{-2-1}{-2+1}|[/m]+
+[m]ln|\frac{0-1}{0+1}|[/m]-lim_( b → -1+0)[m] ln|\frac{b-1}{b+1}|[/m]+
+lim_( c → 1-0)[m] ln|\frac{c-1}{c+1}|-ln|\frac{0-1}{0+1}|[/m]+
+[m]ln|\frac{2-1}{2+1}|[/m]-lim_( d → 1+0)[m] ln|\frac{d-1}{d+1}|=[/m]
=lim_( a → -1-0)[m] ln|\frac{a-1}{a+1}|-ln3[/m]+
+[m]ln1[/m]-lim_( b → -1+0)[m] ln|\frac{b-1}{b+1}|[/m]+
+lim_( c → 1-0)[m] ln|\frac{c-1}{c+1}|-ln1[/m]+
+[m]ln\frac{1}{3}[/m]-lim_( d → 1+0)[m] ln|\frac{d-1}{d+1}|=[/m]